WHICH DISTRIBUTION OF VISIBILITIES?
This section summarizes the results of
Paper II
.
The distribution of samples in Fourier plane that should
be taken as target when optimizing an array for imaging is determined by:
- the "work" that can be demanded to the image reconstruction
process (i.e. the deconvolution algorithm performance and the prior information
available),
- the level of sidelobes tolerated in the clean map,
- the resolution wanted in the clean map.
The work that can be demanded to the imaging process can
be characterized by 2 parameters 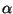 and
and 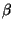 representing respectively the work that can be demanded to the interpolation
and to the extrapolation processes:
representing respectively the work that can be demanded to the interpolation
and to the extrapolation processes:
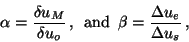
|
(1) |
where
-
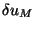 is the sampling accuracy (exact definition in paper
II) required to allow estimation of the visibility function within the sampled
uv-region.
is the sampling accuracy (exact definition in paper
II) required to allow estimation of the visibility function within the sampled
uv-region.
-
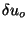 is the Nyquist interval:
is the Nyquist interval: 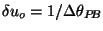 , where
, where 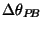 is the angular size of the primary beam.
is the angular size of the primary beam.
-
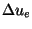 is the radius of the sampled uv-disc.
is the radius of the sampled uv-disc.
-
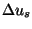 is the radius up to which the visibility function can
be reasonably extrapolated.
is the radius up to which the visibility function can
be reasonably extrapolated.
When no prior information on the source are available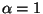 . When mosaicing is possible
. When mosaicing is possible 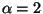 .
.
Let us define the clean weighting function as the
Fourier transform of the wanted clean beam. The level of sidelobes in the
clean map is directly related to the truncation level of the clean weighting
function. Let 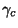 be this truncation level and
be this truncation level and 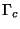 its value in dB. At a given wavelength specifying a resolution is equivalent
to specifying a size for the array. The largest projected baseline of the
array
its value in dB. At a given wavelength specifying a resolution is equivalent
to specifying a size for the array. The largest projected baseline of the
array 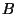 is related to the resolution in the clean map
is related to the resolution in the clean map 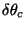 by:
by:
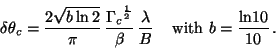
|
(2) |
Then, for an array of 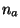 antennas of diameter
antennas of diameter 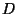 and for a maximum duration of observation in hour
and for a maximum duration of observation in hour 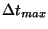 , two characteristic baseline lengths are introduced:
, two characteristic baseline lengths are introduced:
![\begin{displaymath}B_{o}=\frac{ n_a(n_a-1)\,\alpha \,D\,\Delta t_{max}}{48\,\ch......c}\left[\exp\! \left(\frac{b\Gamma_c}{\beta^2}\right)-1\right]\end{displaymath}](img48.gif)
|
(3) |
and,
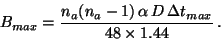
|
(4) |
The first baseline length corresponds to the largest array
size allowing single configuration observations without loss of sensitivity
and the second one to the largest array size allowing single configuration
observations. For larger sizes image reconstruction is in principle not
possible.
For example if we take 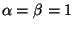 (i.e. no particular deconvolution algorithm and no prior information available),
(i.e. no particular deconvolution algorithm and no prior information available), 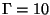 dB and
dB and 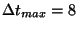 h then we get :
h then we get : 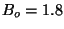 km and
km and 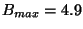 km for 60 antennas of 12 m. For
km for 60 antennas of 12 m. For 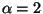 we get
we get 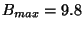 . It is therefore justified for ALMA to build an extended configuration
of 10 km in diameter.
. It is therefore justified for ALMA to build an extended configuration
of 10 km in diameter.
Then three cases have to be considered:
-
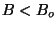 : the array can be optimized for a distribution of samples
equal to the Fourier transform of the wanted clean beam. If the wanted clean
beam is Gaussian then the FWHM,
: the array can be optimized for a distribution of samples
equal to the Fourier transform of the wanted clean beam. If the wanted clean
beam is Gaussian then the FWHM, 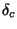 , of the target distribution is given by:
, of the target distribution is given by:
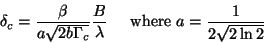
|
(5) |
The duration of the observation required is then given
by:
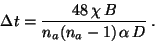
|
(6) |
-
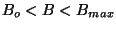 : the duration of observation is maximum. To allow the
uv-disc to be well sampled everywhere and to minimize the loss of sensitivity
the array should be optimized for a wider Gaussian distribution of samples
(for a higher truncation level). The FWHM,
: the duration of observation is maximum. To allow the
uv-disc to be well sampled everywhere and to minimize the loss of sensitivity
the array should be optimized for a wider Gaussian distribution of samples
(for a higher truncation level). The FWHM, 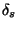 , of the target distribution of samples is solution of:
, of the target distribution of samples is solution of:
![\begin{displaymath}\frac{2 a^2 \lambda^2 \delta_s^2}{B^2}\left[\exp\!\left(\fra......mbda^2 \delta_s^2}\right)-1\right]-{\frac{B}{1.44\,B_{max}}}=0\end{displaymath}](img62.gif)
|
(7) |
-
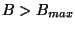 : the array should be optimized for multiconfiguration
observations.
: the array should be optimized for multiconfiguration
observations.
INDEX
| NEXT
| BACK
![]() be this truncation level and
be this truncation level and ![]() its value in dB. At a given wavelength specifying a resolution is equivalent
to specifying a size for the array. The largest projected baseline of the
array
its value in dB. At a given wavelength specifying a resolution is equivalent
to specifying a size for the array. The largest projected baseline of the
array ![]() is related to the resolution in the clean map
is related to the resolution in the clean map ![]() by:
by: ![]() (i.e. no particular deconvolution algorithm and no prior information available),
(i.e. no particular deconvolution algorithm and no prior information available), ![]() dB and
dB and ![]() h then we get :
h then we get : ![]() km and
km and ![]() km for 60 antennas of 12 m. For
km for 60 antennas of 12 m. For ![]() we get
we get ![]() . It is therefore justified for ALMA to build an extended configuration
of 10 km in diameter.
. It is therefore justified for ALMA to build an extended configuration
of 10 km in diameter.