Un Nouvel Univers

F. Combes, Bulletin SFP- Mai 2004

Durant la dernière décennie, notre vision de l'Univers a connu une profonde révolution, due essentiellement aux progrès de la cosmologie observationnelle. Nous savons actuellement que l'Univers est en expansion accélérée, et que sa courbure est nulle. La composition de l'Univers se précise, la matière visible ne représentant qu'une infime partie : nous savons qu'il existe de la matière ordinaire (baryonique) invisible en bien plus grande quantité, et encore plus de matière noire non-baryonique (dont la nature est encore inconnue). Et finalement, le composant qui domine aujourd'hui est la fameuse énergie noire, dont la nature donne naissance à beaucoup de théories encore très spéculatives. De plus, la formation des galaxies et des grandes structures à partir de la soupe primitive régnant juste après le Big-Bang commence à être élucidée grâce aux télescopes de plus en plus puissants, qui permettent de remonter le temps et d'observer l'Univers lorsqu'il n'avait que 4% de son âge, lui-même connu à 1% près, soit 13.7 milliards d'années !
Nous avons maintenant l'espoir de suivre en détail le développement des premières étoiles, terminant l'âge sombre de l'Univers, et initiant sa ré-ionisation.

Comment cette nouvelle vision s'est-elle imposée en quelques années ? Pour mieux le comprendre, il faut rappeler les épisodes précédents. Avant les années 1990, le modèle cosmologique standard (ou Big-Bang) était supposé en expansion monotone décélérée. Tout modèle cosmologique se base sur les équations de relativité générale qu'Albert Einstein a énoncé en 1916, reliant la géométrie de l'Univers à la densité de matière et d'énergie qui le constitue. Dans ces équations, apparaît une constante d'intégration, ou constante cosmologique, qu'Albert Einstein avait introduite afin de permettre un modèle d'Univers stationnaire. Or quelques années après, en 1930, l'expansion de l'Univers fut découverte par Edwin Hubble (voir Encadré 1), et l'univers stationnaire (avec sa constante cosmologique associée) n'avait plus de raison d'être.

Encadré 1

Hubble mesura par effet Doppler la vitesse des galaxies par rapport à nous. Le décalage vers le rouge (redshift) de leur rayonnement, indiquant leur vitesse V, était proportionnel à leur distance D, celle-ci étant mesurée par une série d'indicateurs ou chandelles standard, comme les céphéides (étoiles variables dont la période est une fonction de la luminosité intrinsèque). Les galaxies s'éloignent toutes de nous à une vitesse V = H D, H étant la constante de Hubble. En fonction de l'échelle caractéristique de l'Univers R(t), H = 1/R dR/dt. Sa valeur au temps présent t=0, notée H_o, a longtemps fait l'objet de débats très animés entre différentes écoles européennes et américaines. Aujourd'hui comme nous allons le voir, ce débat a pris fin, et H_o = 72 + 5 km/s/Mpc (les distances étant exprimées en Mpc = 3,3 millions d'années-lumière, et les vitesses en km/s). La détermination de cette constante est fondamentale, car elle permet de déduire l'âge de l'Univers (soit 13,7 milliards d'années), en extrapolant l'expansion dans le passé jusqu'au Big-Bang. Cet âge est compatible avec l'âge des plus vieilles étoiles de notre Galaxie.

Fin d'encadré 1

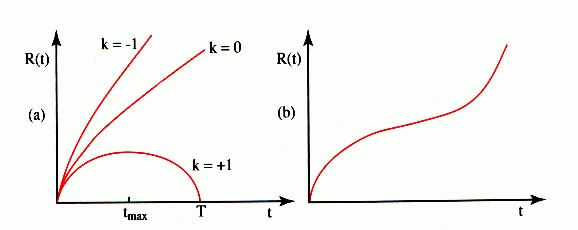
En 1931, Friedmann et Lemaître indépendamment ont déduit, à partir des équations d'Einstein, avec l'hypothèse d'un Univers homogène et isotrope et d'une constante cosmologique nulle, trois catégories de modèles d'Univers, selon sa densité rho par rapport à la densité critique rho_c (rho_c = 3 H²/(8 pi G), soit 10^-29 g/cm³aujourd'hui). Pour des univers denses, soit Omega = rho/rho_c > 1, la courbure de l'Univers est positive, et l'univers est assez dense pour s'effondrer sur lui-même en un Big-Crunch, et retourner l'expansion. Pour la valeur critique de la densité ( Omega = 1), l'expansion est asymptotique, l'univers est plat (courbure nulle). Pour des univers moins denses (Omega < 1), l''expansion est infinie, et la courbure négative (voir Figure 1).

Figure 1, gauche: Evolution de l'échelle caractéristique de l'Univers R(t) pour les trois catégories de modèles de Friedmann-Lemaître (sans constante cosmologique) en fonction du paramètre de courbure k: Ouvert hyperbolique (k=-1), plat parabolique (k=0) et fermé elliptique (k=+1), avec la courbure de l'Univers positive nulle et négative respectivement. Figure 1, droite:
Evolution de R(t) pour un modèle de courbure nulle avec constante cosmologique Lambda. Le comportement est d'abord le même que le précédent cas (k=0), mais l'expansion au lieu de décélérer se retourne, et s'accélère à nouveau. Nous serions dans un tel modèle d'Univers.

La plus importante découverte en cosmologie fut ensuite celle du fonds diffus cosmologique, le rayonnement micro-onde à une température d'environ 3 Kelvin par Penzias et Wilson en 1965. Cette relique du rayonnement chaud du Big-Bang avait été prédite par Gamow en 1946. Pendant longtemps ce rayonnement est apparu complètement isotrope, et la première mesure de ses anisotropies au niveau de Delta T/T ~10^-5 par le satellite COBE en 1992, donna le départ de la révolution actuelle. Depuis de nombreuses expériences au sol ou en ballon, puis le satellite WMAP (NASA) se sont efforcés de cartographier les anisotropies du fonds diffus, ce qui a permis de préciser la géométrie et la composition de l'Univers, comme nous allons le voir ci-après.

Entre temps, dans les années 1970, les astronomes ont apporté de plus en plus de contraintes issues des observations sur la densité de matière de l'Univers : à la fois à l'échelle des galaxies, par leurs courbes de rotation, ou à l'échelle des amas de galaxies, par les mouvements désordonnés des galaxies entre elles, et par les champs de vitesse cosmiques, il est apparu que la matière visible, correspondant à Omega_visible =0.003, était très insuffisante pour rendre compte de la dynamique et de l'équilibre gravitationnel des structures, qui ne pouvaient s'expliquer sans matière invisible. La densité de matière nécessaire dans tout l'univers est de l'ordre de Omega = 0.2-0.3 pour expliquer sa dynamique. Mais la quantité de matière manquante croît avec l'échelle. A l'échelle des galaxies, il suffirait de Omega = 0.03.

La nature de la matière invisible reste encore un des mystères de l'astrophysique moderne. Mais l'on sait qu'une partie est de la matière ordinaire (faite de baryons, protons et neutrons), grâce aux contraintes de la nucléosynthèse primordiale. Dans le premier quart-d'heure suivant le Big-Bang, la température et la densité sont assez fortes pour que les réactions nucléaires puissent former les premiers éléments, comme le deutérium, l'hélium, ou le lithium. La mesure de l'abondance de ces éléments aujourd'hui (notamment le deutérium qui est détruit ensuite dans les étoiles), permet de contraindre la densité de baryons dans l'Univers, à environ Omega_b = 0.05 (cette limite dépend des autres paramètres de l'Univers comme H_o, mais nous simplifions délibérément ici, ces paramètres devenant de plus en plus précis). Si toute la matière noire pourrait encore être baryonique à l'échelle des galaxies, ce n'est plus vrai à l'échelle des amas de galaxies ni de l'Univers en entier.

D'autre part, la formation des galaxies et des grandes structures ne peut pas se produire si la matière est uniquement baryonique, car les baryons restent couplés au rayonnement avant la recombinaison de l'Univers, qui se produit 380 000 ans après le Big-Bang. A cet époque, la température de l'Univers est tombée assez bas pour que les électrons et les protons se re-combinent en atomes d'hydrogène neutre, et les photons du fond diffus se découplent de la matière baryonique, qui peut alors s'effondrer sous l'effet de sa propre gravité. Mais l'expansion de l'Univers ralentit cet effondrement, et il est déjà trop tard pour former les galaxies. Par contre, si l'essentiel de la matière noire est non-baryonique (de nature encore inconnue, mais n'interagissant pas avec les photons), alors les condensations gravitationnelles peuvent démarrer bien avant. Les photons ne peuvent pas stopper leur effondrement, comme pour les baryons. A la recombinaison, les baryons tombent dans les halos de matière noire déjà formés, et les galaxies peuvent exister aujourd'hui.

Encadré 2: Matière noire baryonique

Etant donné que la matière visible ne représente que Omega = 0.003, et Omega_b = 0.05, il nous reste à découvrir où sont passés tous les baryons! Des programmes de recherches par micro-lentilles gravitationnelles (MACHOS, EROS, OGLE) ont été entrepris dans la dernière décennie pour essayer de détecter des objets compacts autour de notre Galaxie qui, bien qu'invisibles, pourraient dévier la lumière d'étoiles d'arrière-plan. Les principaux candidats étaient des naines brunes, sortes de gros Jupiters avec une masse juste trop petite pour faire des étoiles. En fait, la masse ainsi détectée est largement insuffisante, et l'hypothèse la plus probable aujourd'hui est que la matière noire baryonique est sous forme de gaz diffus, soit chaud entre les galaxies, ou très froid, moléculaire, associé aux galaxies.

Fin d'encadré 2

Dans les années 1980, une intense activité théorique a permis d'apporter d'autres contraintes à la nature de la matière noire non-baryonique : celle-ci pouvait être chaude (HDM ou Hot Dark Matter), ou froide (CDM, Cold Dark Matter), selon que les particules correspondantes se découplent du plasma primitif lorsqu'elles sont encore relativistes (faibles masses, comme les neutrinos), ou non (plus grandes masses, comme les neutralinos, de masse supérieure à 10 fois celle du proton). Les simulations numériques ont montré que seule la matière froide s'effondrait suffisamment vite pour former les galaxies.

Enfin, le modèle classique du Big-Bang se heurtait à plusieurs paradoxes, qui ont amené la théorie de l'inflation (Guth 1981, Linde 1983). Un des paradoxes est celui de l'horizon : aujourd'hui nous observons le fond micro-onde de rayonnement cosmologique pratiquement homogène et isotrope, or ces photons proviennent de la dernière surface de diffusion (dernière interaction avec la matière) correspondant à la recombinaison, 380 000 ans après le Big-Bang. A cette époque, l'horizon était tout petit, 380 mille années-lumière, et les photons que nous voyons provenir de deux régions différentes du ciel ne devraient pas être causalement reliés. Pourquoi sont-ils alors à la même température, à 10^-5 près ?

L'inflation résoud le problème en supposant que l'Univers a traversé très tôt dans son histoire (à t~10^-32s) une période d'expansion exponentielle, ou le rayon caractéristique de l'univers a augmenté de 30 ordres de grandeur en une fraction de seconde. Cette phase peut être décrite par une constante cosmologique très grande, ou la pression a un signe opposé à la densité (effet répulsif), d'où l'expansion exponentielle. C'est l'énergie du vide quantique qui est responsable de l'inflation, et ces fluctuations du vide deviennent fluctuations de densité lorsque l'énergie du vide se transforme en matière et rayonnement. L'homogénéité de l'Univers à l'intérieur d'une bulle ainsi étirée est assurée. La théorie de l'inflation implique un univers globalement plat. L'avantage est aussi de prédire l'origine des fluctuations primordiales, dont la valeur est déterminée par les constantes fondamentales de la physique des particules. L'inflation a permis d'agrandir les fluctuations microscopiques (de taille subatomique) d'origine quantique à des tailles macroscopiques.

L'origine des fluctuations primordiales pourrait aussi s'expliquer par les défauts topologiques qui surviennent encore plus tôt (à t~10^-36s) dans une transition de phase cosmologique associée avec des brisures spontanées de symétrie dans la théorie qui unifie forces fondamentales et particules. Selon la nature de la brisure de symétrie, les défauts topologiques peuvent être un monopôle, une corde cosmique (une dimension) ou des textures à 2 ou 3 dimensions dans l'espace-temps.

Voilà où nous en étions à l'aube des années 1990. La théorie de l'inflation requérant une courbure nulle, l'Univers était supposé rempli de matière, à la densité critique Omega =1, contrairement aux évidences à petite et grande échelles. Au moins trois grandes catégories d'observations vont bouleverser ce modèle :

L'observation des anisotropies du fond cosmologique
L'observation des supernovae de type Ia
L'observation des lentilles gravitationnelles

1-- Les anisotropies du fond cosmologique :

Tout a commencé avec la détection par le satellite COBE de la NASA des anisotropies du fonds cosmologique de rayonnement micro-onde, avec une amplitude de l'ordre de 10^-5. Cette mesure est difficile et suppose une très bonne soustraction des rayonnements d'avant-plan, c'est pourquoi le satellite COBE a fait une cartographie de tout le ciel à plusieurs longueurs d'onde, de la radio à l'infra-rouge proche et l'optique, afin de séparer les divers rayonnements par leur signature spectrale. Le fonds micro-onde CMB (ou Cosmic Microwave Background), domine le rayonnement de l'Univers à 1mm de longueur d'onde : le ciel est très homogène dans ce domaine ; une fois soustrait un fonds constant, on découvre une perturbation dipolaire qui est la trace de notre mouvement par rapport au référentiel absolu du corps noir. La galaxie se déplace à environ 600km/s par rapport au CMB, ce mouvement étant expliqué par la présence d'amas de galaxies qui jouent le rôle d'attracteurs dans le voisinage. Une fois soustrait ce dipôle, on découvre enfin le rayonnement de la Galaxie, qui a une géométrie tout à fait particulière dans le référentiel galactique (cf figure 2). Ces rayonnements d'avant-plan sont soustraits, pour mettre en évidence les fluctuations du CMB, pratiquement dans toutes les directions du ciel. Ces fluctuations représentent les perturbations qu'ont subi les photons lors de la dernière surface de diffusion, lors de la recombinaison de l'Univers, et nous pouvons mesurer ainsi l'amplitude des fluctuations au début de l'Univers qui ont donné lieu aux grandes structures par la suite. La résolution spatiale des instruments de COBE n'était que de 7 degrés d'arc dans ce domaine de longueurs d'onde, ce qui ne contraint que les fluctuations à très grandes échelles.

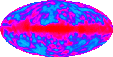
Figure 2a:
Carte du ciel à 3mm de longueur d'onde par le satellite COBE. A gauche: la carte brute est un fond très homogène puis de gauche à droite , le dipôle dû au mouvement de notre Galaxie, après soustraction du fond homogène. Au milieu, émission de la Voie Lactée après soustraction du dipôle, et à droite: carte des fluctuations de température, une fois soustraite les émissions d'avant-plan.

Figure 2b:
Carte des fluctuations de température du fonds micro-onde cosmologique (CMB) à plus haute résolution spatiale avec WMAP.

Les fluctuations de température dans le fonds CMB sont dues à des fluctuations de densité de matière. Juste avant la recombinaison des protons avec les électrons, les baryons sont étroitement couplés avec les photons, et toute instabilité gravitationnelle est empêchée par la pression des photons: le fluide baryons-photons est stable et les ondes qui le parcourent sont des ondes acoustiques. Cette physique est linéaire et très bien connue, les prédictions font l'objet des courbes de la Figure 3, selon les valeurs des paramètres cosmologiques et de l'origine des fluctuations primordiales. C'est justement parce que la physique est simple que les observations du CMB sur tout le ciel peuvent nous donner beaucoup d'informations sur les paramètres de l'Univers.

Dans la courbe de la Figure 3, le plateau à grande échelle ( l < 100) correspond à des oscillations de période plus grande que l'âge de l'Univers à l'époque de la recombinaison (ou des longueurs d'onde supérieures à l'horizon); si le spectre de fluctuations est invariant d'échelle, comme le prédisent les théories de l'inflation, alors la courbe est effectivement plate. Les observations de COBE ont permis de donner la hauteur du plateau. Entre 100 < l < 1000, les oscillations du fluide baryons-photons ont le temps de se produire. Les fluctuations de densité s'accompagnent de compression/raréfaction et de vitesses maximales/minimales du fluide et la température du CMB varie par effet Doppler, aussi ces pics sont appelés les pics Doppler. Enfin aux très petites échelles (l > 2500) les oscillations sont amorties car la surface de dernière diffusion a une certaine épaisseur. En fait la recombinaison de l'Univers n'est pas instantanée, mais s'étale dans le temps, et l'on moyenne sur la ligne de visée plusieurs surfaces, et les différents signaux sinusoidaux s'annulent mutuellement.

La position sur l'axe des l du premier pic Doppler dépend essentiellement de la somme Omega + Omega_Lambda, soit de la courbure de l'Univers (dans les mêmes unités, le paramètre de courbure s'exprime par Omega_k, et Omega + Omega_Lambda + Omega_k=1). Déjà les expériences montées sur ballon (Boomerang en 2000, Archéops en 2002) avaient montré que l'Univers était plat, avec Omega + Omega_Lambda =1 (i.e. Omega_k =0). Ceci fut confirmé en 2003 par les résultats encore plus précis du satellite WMAP. Le rapport d'intensité entre les deux premiers pics Doppler est très sensible à la densité de matière baryonique Omega_b: les différentes expériences ont permis de préciser cette valeur et confirmer la valeur prédite par la nucléosynthèse primordiale, une fois la constante de Hubble connue (Figure 4).

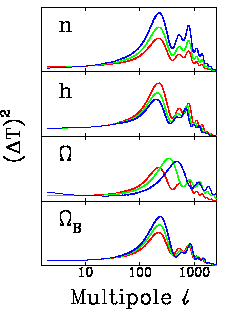
Figure 3:
Intensité des fluctuations, en fonction du multipôle l (les fluctuations de température Delta T/T (theta, phi) sont habituellement décomposées en harmoniques sphériques Y_lm(theta, phi). Les grandes valeurs de l correspondent aux hautes fréquences spatiales, soit aux petites échelles angulaires, approximativement l ~100deg/ theta. Les séparations angulaires theta représentent une taille sur la dernière surface de diffusion (correspondant au redshift z~1000), qui correspondent à des tailles aujourd'hui agrandies d'un facteur 1000 par l'expansion, soit environ 200 Mpc par degrés. Ainsi les fluctuations de densité qui ont donné naissance aux galaxies (1 Mpc) correspondent à des échelles angulaires de 0.3 minute, celles des amas de galaxies (20 Mpc) de 6 minutes d'arc.

A gauche: plusieurs modèles d'Univers, montrant les variations des fluctuations de température du CMB avec les divers paramètres: dans chaque boîte, la courbe rouge est le modèle standard de courbure nulle, avec Omega = 1, H_o = 50km/s/Mpc, Omega_b = 0.08 et n=1. Les autres courbes montrent l'effet de varier de façon continue (de rouge vers le bleu), n la pente du spectre de fluctuations primordiales, h la constante de Hubble, Omega la densité de matière, et Omega_b la densité de baryons (d'après Bennett, Turner and White 1997, Physics Today Nov, p.32)

A droite: Mesures des fluctuations de température par plusieurs expériences, dont Archéops (cf site web-Archéops, 2003).

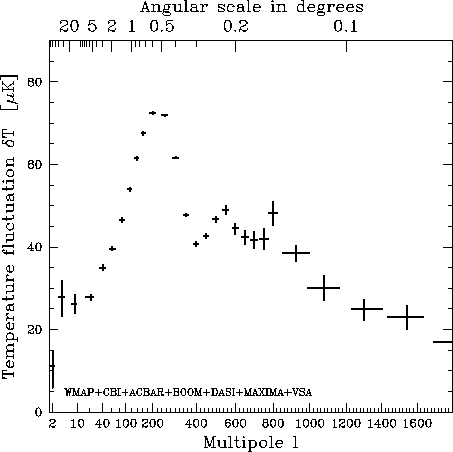
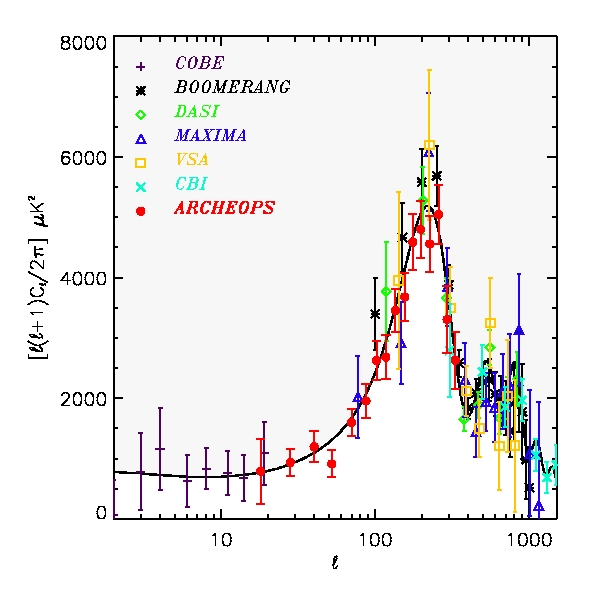
Figure 4:
Mesures de l'intensité des fluctuations du CMB, synthétisées et moyennées pour les diverses expériences récentes, incluant le satellite WMAP

(compilation par Tegmark et al 2003, http://www.hep.upenn.edu/~max/cmb/experiments.html).

Parmi les nouveaux résultats apportés par l'étude des anisotropies du CMB par WMAP est la quantification de la quantité de gaz ionisé que traverse la ligne de visée avant de voir la dernière surface de diffusion. Les fluctuations de température sont en effet en partie brouillées par la diffusion de 20% des photons initiaux. Ceci indique que la ré-ionisation de l'Univers par les premières étoiles a commencé très tôt, environ 200 millions d'années après le Big-Bang.

2-- Les supernovae de type Ia

La première indication directe de la présence d'une constante cosmologique ou d'une composante d'énergie noire, en plus de la matière noire, est venue de l'observation des supernovae en 1998 par deux équipes concurrentes (Riess et al 1998, Perlmutter et al 1999). Les supernovae de type Ia ne sont pas des explosions dues à l'effondrement gravitationnel d'étoiles massives en fin de vie (comme les types II), mais les explosions thermonucléaires de naine blanche dans un système binaire, qui reçoit de la matière par son compagnon. La naine blanche composée de carbone-oxygène essentiellement explose proche de la masse de Chandrasekhar¹, et l'on conçoit que les phénomènes physiques associés conduisent toujours à des luminosités comparables, quel que soit le système précurseur, et la façon d'accréter de la matière. Les supernovae de type Ia peuvent donc être utilisées comme des chandelles standard, afin de déterminer les distances d'objets très lointains dont on connaît le redshift. En pratique, ce ne sont pas tout à fait des chandelles standard, mais les observations ont montré qu'il existait une bonne corrélation ente la forme de la courbe de lumière d'une SN Ia et sa luminosité au maximum. La méthode consiste donc à observer et échantillonner suffisamment la courbe de lumière des SN Ia, qui s'étale sur plusieurs semaines, et d'en déduire ensuite la luminosité maximum standard, la dispersion n'étant alors pas plus de 15%.

La performance des télescopes actuels permettant d'observer ces SN Ia jusqu'à de grandes distances (redshift jusqu'à z=1), la géométrie de l'Univers peut être explorée. La figure 5 montre le diagramme de Hubble, c'est-à-dire la luminosité "standardisée" en fonction du redshift des SN Ia, en comparaison avec la prédiction de plusieurs modèles d'Univers. La luminosité des SN Ia est observée plus faible que l'on attendrait avec un modèle d'Univers en expansion décélérée. Il faut donc que l'expansion soit accélérée et les distances plus grandes (amenant à l'existence de la constante cosmologique Lambda. Les effets de l'extinction par la poussière ne sont pas capables de rendre compte de l'affaiblissement de la luminosité, car en fait les couleurs des SN Ia ne sont pas rougies, et d'autre part, à grand redshift la luminosité des SN Ia remonte au contraire, ce qui va dans l'autre sens. Cet effet est attendu, car avant de ré-accélérer, l'expansion se décélérait: l'influence de la constante cosmologique sur la matière n'est dominant qu'à bas redshift.

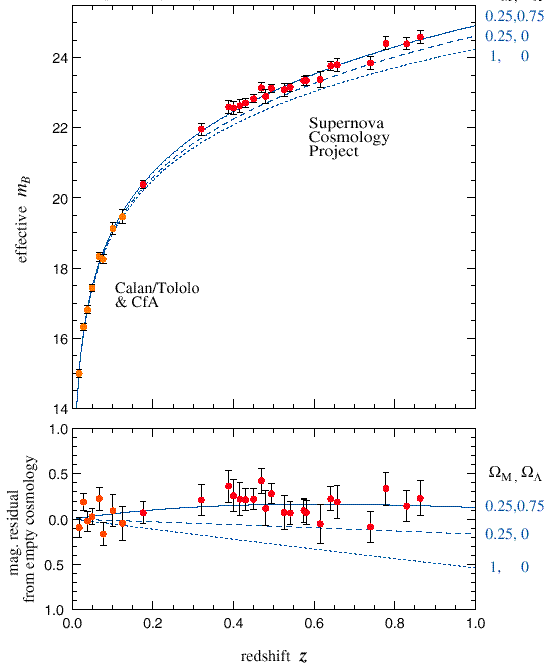
Figure 5:
Diagramme de Hubble des SN Ia selon Knop et al (2003). En haut: Magnitudes apparentes des SN Ia "standardisées" en fonction du redshift z. Les points sont portés en rouge, avec leurs barres d'erreur, les courbes sont les prédictions des modèles ( Omega_M, Omega_Lambda). En bas: Résidus des magnitudes par rapport à un modèle d'univers vide (d'après Knop et al 2003).

3-- Les lentilles gravitationnelles

La déviation des rayons lumineux par la matière est un outil incomparable, qui permet de tracer toute la matière sur la ligne de visée, y compris la matière invisible. Le phénomène de lentille peut former plusieurs images d'un même objet ponctuel d'arrière plan, lorsque les rayons lumineux passent très près d'un objet massif. Mais ce phénomène de lentille forte est relativement rare et ne permet pas de tracer la masse à grande échelle. La présence d'un amas de galaxies produit des arcs de lumière, qui sont les images de certaines galaxies de fond complètement déformées, car se trouvant près des caustiques (Figure 7). Par contre, le phénomène de lentille faible, ou cisaillement gravitationnel, correspond à la déformation cumulée sur la ligne de visée par toute la matière à grande échelle, et se manifeste par une ellipticité plus grande des galaxies d'arrière-plan. Cette déformation gravitationnelle ne peut se détecter que statistiquement sur un grand nombre de galaxies, et fait l'objet aujourd'hui de plusieurs cartographies à grande échelle.

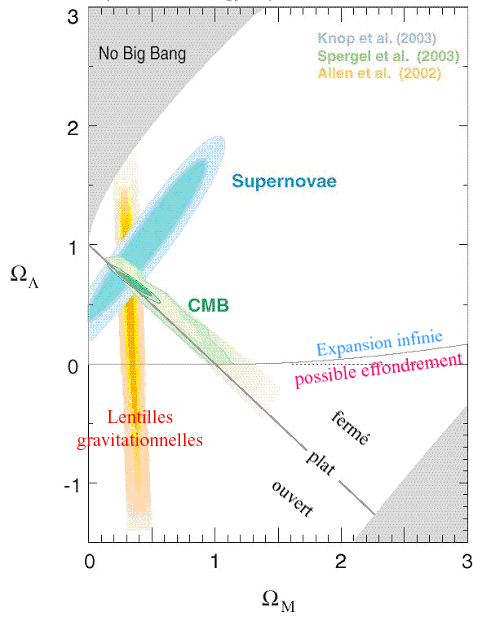
Figure 6:
Contours de confiance dans le diagramme Omega_M, Omega_Lambda synthétisant les contraintes amenées par le CMB, en vert, les SN Ia, en bleu, et les lentilles gravitationnelles, en orange (d'après Knop et al 2003). Cette dernière contrainte est obtenue grâce aux déformations en arcs des galaxies d'arrière-plan devant des amas de galaxies jouant le rôle de lentille (Allen et al 2002).

Ces cartographies vont permettre de mieux contraindre le paramètre de densité de matière Omega, de même que le spectre de distribution de la masse à différentes échelles, essentiel pour connaître comment se sont formées les galaxies et les grandes structures, et approcher la nature de la matière noire. Associé avec la détermination de la platitude de l'Univers par les mesures du CMB, ce résultat permet de donner une valeur de Omega_Lambda, en accord avec la détermination directe des supernovae (cf Figures 6 et 8).

Figure 7:
Arcs gravitationnels dans l'amas de galaxies Abel 2218, image obtenue avec le Hubble Space Telescope (HST, Fruchter et al 2001).

Le mystère de l'énergie noire: constante cosmologique ou quintessence?

Le terme de constante cosmologique Lambda, qui prend dans notre nouvelle vision de l'Univers, une importance considérable, peut être interprété de différentes manières. Comme son nom l'indique, c'est une constante en fonction du temps dans les équations d'Einstein, et la densité d'énergie "équivalente", c'est-à-dire rho_Lambda = Lambda/( 8 pi G) (avec G la constante de gravitation) est aussi une constante. Par contre, l'élément sans dimension, donnant son importance relative dans la courbure de l'Univers, Omega_Lambda = 8 pi G rho_Lambda / 3 H² dépend du temps, car la constante de Hubble H(t) en dépend. C'est aussi le cas pour la densité de matière rho_M, pour laquelle Omega_M = 8 pi G rho_M / 3 H², mais contrairement à rho_Lambda, la densité de matière n'est pas constante dans le temps, mais décroît avec l'expansion du rayon caractéristique de l'Univers R(t) comme rho_M ~R^-3. Il est donc évident que le terme en Lambda devient dominant dans l'Univers que tout récemment, puisqu'il est au temps présent trois fois plus grand que celui de matière. A l'époque de la formation des galaxies par exemple, il était négligeable, il n'est devenu comparable au terme de matière qu'il y a 5 milliards d'années environ. C'est à ce moment là que l'expansion commence à se retourner et se ré-accélérer. Ce retournement a peut-être été déjà vu avec la méthode des supernovae (Figure 5).

Le terme de constante cosmologique peut donc être interprété comme un fluide totalement homogène, de densité constante, et de pression négative, donc ayant un effet répulsif. La force agissant sur l'entourage est une force proportionnelle à la distance d et positive (contrairement à la force de gravitation, négative et en 1/d²). Même au temps présent, son importance au niveau des galaxies et des amas de galaxies est très faible.

Comme ces caractéristiques sont tout à fait comparables à celles de l'énergie du vide², il est intéressant de savoir ce que prédirait la physique quantique: en fait, si on intègre les énergies minimum selon la théorie des champs (et selon les troncatures adoptées), on trouve une constante entre 55 et 123 ordres de grandeur supérieure à ce qu'il faudrait! Sans doute des termes doivent compenser, l'énergie se désintégrer, ou une symétrie fondamentale annuler cette énergie du vide. Pour l'instant, c'est une impasse pour la théorie.

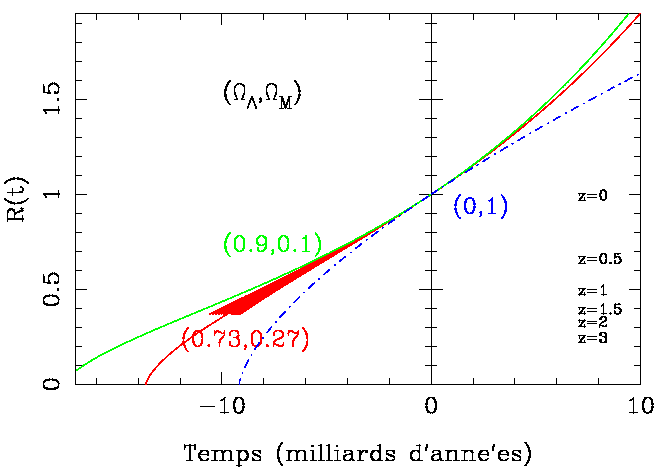
Figure 8:
Evolution de R(t) pour le modèle le plus favorisé par les données observationnelles aujourd'hui (en rouge). Les deux chiffres entre parenthèses indiquent pour chaque modèle de courbure nulle Omega_Lambda et Omega_M (matière). Les redshifts z correspondant à chaque époque sont indiqués à droite ((1+z)= 1/R(t)). L'espace colorié en rouge correspond à la région où les SN Ia ont été observées. Compte-tenu de toutes les contraintes du CMB et des lentilles gravitationnelles, le meilleur modèle correspond à Omega_Lambda = 0.73, Omega (matière non-baryonique)= 0.22, Omega_b = 0.05.

Etant donné ce désaccord, d'autres idées théoriques ont été proposées. Puisque l'énergie noire et la matière semblent avoir des importances comparables seulement aujourd'hui, cette coincidence fait penser à un hasard un peu trop heureux, ou alors le fameux terme Lambda n'est pas une constante, mais varie aussi avec le temps. Il ne s'agit plus alors d'une constante cosmologique, ou énergie du vide, mais bien d'un autre terme à rajouter à la physique, sous forme d'un champ scalaire par exemple. Sans que l'on sache vraiment de quelle nature est cette physique il s'agirait d'un cinquième élément, ou "quintessence" (les quatre premiers connus étant les photons, les neutrinos, les baryons, et les particules formant la matière non-baryonique). Plusieurs formes de champ scalaire ont été proposées, et ce domaine est très actif en physique théorique actuellement: les modèles se distinguent par l'équation d'état de la quintessence, car la relation entre la densité d'énergie et sa pression n'a plus besoin d'être celle de l'énergie du vide ou de la constante cosmologique (i.e. P = - rho, dans un système d'unité où la vitesse de la lumière c=1). Le paramètre w est introduit, pour quantifier le rapport P/rho. Les contraintes observationnelles aujourd'hui permettent des valeurs de w entre -1 et -0.5. Il serait intéressant si ce champ scalaire pouvait à la fois prévoir l'inflation et la quintessence, des théories basées sur les dimensions supplémentaires à 3+1 pour la matière ou théories des branes sont aussi proposées. De même des théories essayant de coupler matière noire et énergie noire sont à l'étude. Certaines hypothèses ont déjà été éliminées par les observations: notamment l'explication de l'énergie noire par les défauts topologiques de l'Univers, comme les parois de domaines.

L'époque précise de l'Univers où l'expansion se retourne, et se ré-accélère dépend de w, et les futures missions qui se proposent de mesurer des milliers de SN Ia à diverses époques en remontant dans le temps de 8 milliards d'années, pourront déterminer précisément l'équation d'état: il est prévu de détecter avec la caméra grand champ du télescope CFHT (Canada-France-Hawaii) 2000 supernovae entre 2003 et 2008 et encore bien plus avec le futur télescope spatial dédié SNAP (SuperNovae/Acceleration Probe). Il sera même possible de déterminer si le paramètre w de l'équation d'état varie avec le temps, w(t), ce qui permettrait alors d'imaginer que l'accélération de l'expansion de l'Univers observée aujourd'hui ne soit pas inéluctable, et que l'Univers s'arrête de se diluer, et même se re-condense un jour.

¹ Une naine blanche est en équilibre, car la pression de Fermi de dégénérescence des électrons compense l'attraction gravitationnelle. Cet équilibre n'est possible qu'en-dessous d'une masse critique de 1,4 Masses solaire, limite calculée la première fois par Chandrasekhar.

² L'existence d'une énergie non-nulle du vide correspondant aux fluctuations quantiques, par création de paires virtuelles particules-antiparticules, a été prédite par Casimir en 1948, et vérifiée par de nombreuses expériences de laboratoire.

Pour en savoir plus

Introduction à la physique du CMB, par Wayne Hu

http://background.uchicago.edu/~whu/beginners/introduction.html

Site de la mission européenne Planck

http://astro.estec.esa.nl/Planck/

Site de WMAP (NASA)

http://map.gsfc.nasa.gov/m_mm.html

Site de Archéops

http://journal.archeops.org/First_results/

The Elegant Universe : Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory, par Brian Greene, Vintage, 2000

Gravitational lenses, par E.E. Falco, Springer, 1999

Site des lentilles gravitationnelles de l'IAP:

http://www2.iap.fr/LaboEtActivites/ThemesRecherche/Lentilles/LentillesTop.html

The Accelerating Universe : Infinite Expansion, the Cosmological Constant, and the Beauty of the Cosmos, par Mario Livio, John Wiley & Sons, 2000

Site FROGS FRench Observing Group of Supernovae

http://supernova.in2p3.fr/doc/accueil.html

Site SCP: Supernovae Cosmology Project

http://panisse.lbl.gov/

Basics of Modern Cosmology

Dolgov, Sazhin and Zeldovich, Editions Frontières, 1990

Galaxies and Cosmology

Combes, Boissé, Mazure and Blanchard, Springer, 2002

Références des articles

Allen, S. W., Schmidt, R. W., Fabian, A. C.: 2002, MNRAS 334, L11

Guth A.: 1981 PhRvD 23, 347

Knop R.A. et al. : 2003 ApJ 598, 102

Linde A.: 1983, JETP Letters, Vol 38, p.176

Perlmutter S. et al.: 1999 ApJ 517, 565

Riess A.G. et al.: 1998 AJ 116, 1009

Spergel D.N. et al. : 2003 ApJS 148, 175


Figure 1, gauche: Evolution de l'échelle caractéristique de l'Univers R(t) pour les trois catégories de modèles de Friedmann-Lemaître (sans constante cosmologique) en fonction du paramètre de courbure k: Ouvert hyperbolique (k=-1), plat parabolique (k=0) et fermé elliptique (k=+1), avec la courbure de l'Univers positive nulle et négative respectivement.	Figure 1, droite: Evolution de R(t) pour un modèle de courbure nulle avec constante cosmologique Lambda. Le comportement est d'abord le même que le précédent cas (k=0), mais l'expansion au lieu de décélérer se retourne, et s'accélère à nouveau. Nous serions dans un tel modèle d'Univers.


Figure 2a: Carte du ciel à 3mm de longueur d'onde par le satellite COBE. A gauche: la carte brute est un fond très homogène puis de gauche à droite , le dipôle dû au mouvement de notre Galaxie, après soustraction du fond homogène. Au milieu, émission de la Voie Lactée après soustraction du dipôle, et à droite: carte des fluctuations de température, une fois soustraite les émissions d'avant-plan.

Figure 2b: Carte des fluctuations de température du fonds micro-onde cosmologique (CMB) à plus haute résolution spatiale avec WMAP.