Scintillation of pulsars observed at radio frequencies through the turbulent ionized interstellar medium

Simulation of the interstellar scintillation and the extreme scattering events of pulsars
Hamidouche, M., Lestrade, J.-F., 2007,
A&A, 468, 193, (astro-ph/0703641)

We are simulating scintillation of pulsars observed at radio frequencies through a turbulent ionized interstellar medium. In collecting a large ensemble of data, Amstrong, Rickett and Spangler (1995, Ap.J., 443, 209) have found that the electron density fluctuations of the ionized interstellar medium have a turbulent Kolmogorov 3-dimensional power spectrum between the scale 10 ⁶ m and 10 ¹⁸ m. This prompted us to investigate by means of a simulation if this turbulence could be responsible for the Extreme Scattering Events (ESE) that have been observed in the monitoring of the intensity of the millisecond pulsars 1937+21 (Lestrade, Rickett and Cognard, 1998, A &A, 334, 1068) and J1643-1224 (Maitia, Lestrade, Cognard, 2003, Ap.J., 582, 972) at the radiotelescope at Nancay, France. ESE's were also and first discovered in directions of extragalactic sources at radio frequencies by Fiedler et al (1987). This simulation work is conducted by Jean-Francois Lestrade (Observatoire de Paris) and Murad Hamidouche (formerly at LPCE, Orléans, France, and now at University of Urbana-Champagne, Illinois).

Schematics for the computation conducted in Physical Optics with the Kirschoff-Fresnel Integral

Simulted Pulsar Dynamical Spectra at 1.41 GHz with turbulence Cn2 = 10-3 m-20/3

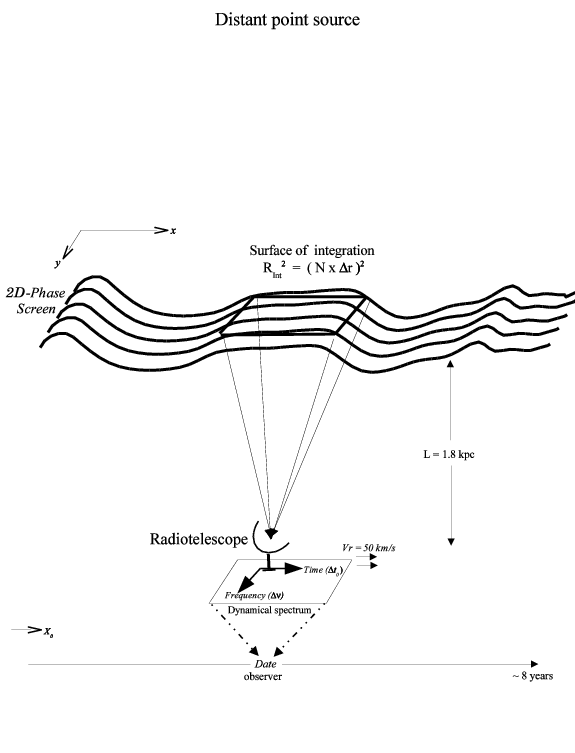
Figure 1: Series of 16 simulated dynamical spectra (time-frequency domain) of the pulsar 1937+21 when a turbulent screen intervenes on the line of sight. Turbulence is characterised by the 3N Kolmogorov power spectrum P3N(q) =Cn2 q -11/3 with the strength Cn2 = 10-3 m-20/3, i.e. the coherent length is 2.66 107 m. The median frequency of these dynamical spectra is 1.41 GHz (lambda=21 cm), their bandwidth is 8 MHz sampled over 32 channels (horizontal scale) and the integration time is 70 minutes, when the screen speed is 50 km/s, sampled over 32 bins (vertical scale). These 16 dynamical spectra are 2.5 days apart with this screen speed. The Fresnel scale is 4.8 109 m with the screen placed at mid-distance to the pulsar (1.8 kpc). In these conditions, the computation of the phase screen can be reduced to the thin screen approximation. Each dynamical spectrum in the observer plane has to be calculated with the general Fresnel-Kirchhoff integral which was computed numerically with 1/4 of the coherence length (6.5 106 m) as the integration step in the screen plane. The surface of integration over the phase screen is as large as 21916 x 21916 pixels and the oberver plane is as large as 32 frequency-channels x 32 time-bins as already mentioned. The pulsar is assumed a point source. Note that all 16 spectra are displayed here with the same intensity scale. The "speckles" in these dynamical spectra have mean sizes of 9 minutes and 0.75 MHz comparable to the values observed (6.2 minutes and 0.56 MHz) for 1937+21 at 1.41 GHz by Ryba (1991, PhD Dissertation, p.58)

Figure 2: (Left) Simulated intensity of 1937+21 at 1.41 GHz in the observer plane over 6 months from a 131k x 131k square phase screen. Each intensity point is the average intensity over a dynamical spectrum. The limited integration time (70 min) and integrated bandwidth (8 MHz) at the telescope make both diffractive scintillation, on a few minute time scale, and refractive scintillation, on a few month time scale, apparent in the observation and need to be computed simultaneously. The resulting intensity autocorrelation function (Right) shows that the refractive scale is about 15 days. This value is consistent with the one expected for the Kolmogorov turbulence power spectrum and Cn2 = 10-3 m-20/3.

Computation :
The computation of each dynamical spectrum of Figure 1 took 40 hours on one 400 MHz processor of an Enterprise 3500 Server SUN/SOLARIS 9 and the intensity curve of Figure 2 took 4 months as a background task on this machine made continously running by Djilali Zidani at Observatoire de Paris/LERMA. Data storage for the phase screen was 50 GBytes, permanently, but required a peak storage of 200 Gbytes during its construction.

Concluding remarks at this stage:
Various events in the intensity curve at 1.41 GHz of Fig 2 (Left) could be regarded as short-lived Extreme Scattering Events.In order to reach a conclusion, we are presently densifying the simulation at 1.4 GHz and extending it to 1.7 GHz to see if this is a broad band phenomenon as observed during Extreme Scattering Events.



Contact Jean-François Lestrade about this page.