-
A concise review of the Iranian calendar
M. Heydari-Malayeri
Paris Observatory
PDF format
Version française
Persian version
1. Introduction
The Iranian, or Persian, calendar is solar, with the particularity that the year is defined by two successive, apparent passages of the Sun through the vernal (spring) equinox. It is based on precise astronomical observations, and moreover uses a sophisticated intercalation system, which makes it more accurate than its younger European counterpart, the Gregorian calendar. It is currently used in Iran as the official calendar of the country. The Iranian calendar has a long, multi-millennial history with deep roots in the Persian culture, in particular the Zoroastrian heritage. Although this paper does not intend dealing with the history of the Iranian time reckoning because the questions addressed do not make it necessary, it presents a brief summary of its most remote origins. Interested readers can find detailed information on this subject in, e.g., Taqizâdeh (1938), Birashk (1993), Encyclopedia Iranica, and Abdollâhi (1996). The present version of the calendar results from a reform led by the famous astronomer, mathematician, and poet Omar Khayyâm (1048-1131 Christian era, hereafter A.D.: Anno Domini) which took place at the vernal equinox of A.D. 1079 (Friday, 21 March; see below Note 1), corresponding to the 1st of Farvardin of A.P. (Anno Persico) 458. The calendar was also called Jalâli, from the name of the ruler who ordered the reform. In modern times, its principles were officially adopted by the Iranian parliament on 31 March 1925 (11 Farvardin A.P. 1304).
The new year festival, called Nowruz, from Persian now "new" + ruz "day", is also a Zoroastrian legacy with many cultural significances, symbolizing the awakening or rebirth of the natural life after barren winter (Note 2). It is accompanied, several days or weeks before and after the spring equinox, by joyful ceremonies carrying centuries-old traditions. We can, for example, mention the house cleaning and seed sprouting before the Nowruz arrival and the fire festivity on the eve of the last Wednesday of the year as well as the mass picnic to verdant countryside on the 13th day of the new year. There are other celebrations, but their discussion is out of the scope of this paper. Nowruz has been celebrated for several millennia by all the peoples living in the Western and Central Asia (Afghans, Azeris, Caucasians, Kazakhs, Kurds, Kyrgyz', Tajiks, Turkmens, and others) regardless of ethnicity, religion, or language. Apart from its profound message, the non-ethnic and non-religious characteristics of Nowruz seem to be the main reasons why it has been cherished as a common cultural heritage by so many peoples with different backgrounds.
In spite of its outstanding status, mainly its precision and rationalistic characteristic of relying on detailed astronomical observations, the Iranian calendar is poorly known in the West. In fact, few studies have so far analyzed the basic elements of its system in the light of modern astronomical findings, although several works have addressed the historical origins of the calendar. In particular, the true value of the length of the year in the Iranian calendar should be emphasized, since nowadays there is a widespread confusion between the concepts of the modern ``tropical'' year and the vernal-equinox year upon which the Iranian calendar is based. A misinterpretation of this topic may upset the intercalation system and affect the accuracy of the calendar. One of the goals of this paper is therefore to clarify this point.
The paper is not only aimed at calendar experts but effort has been made to be accessible by non specialists. It is organized as follows. After this Introduction, Section 2 presents a general description of the Iranian calendar. Then, in Section 3, we define the year and discuss its length using the results from recent astronomical research. In Section 4 we underline the difference between the ``tropical'' and Iranian years, while the intercalation system, based on the 33-year cycle, is described in Section 5. Although the paper is mainly interested in the astronomical background of the Iranian calendar, historical aspects are not overlooked and, in particular, Section 6 presents a brief note regarding the history of the reform led by Khayyâm. In recent years, some Iranian calendar experts have suggested the presence of a 2820-year cycle in the Iranian calendar. We discuss this issue in Section 7 and point to the flaws of this scheme. The correspondence between the Iranian and other calendar systems is dealt with in Section 8, and Section 9 presents some remarks on the ancient origins of the Iranian calendar. Finally, the conclusions are given in Section 10. Throughout the paper, complementary explanations are given in 16 notes which appear at the end of the article.
2. General description
Nowruz starts at the precise instant when the Sun, in its apparent annual course on the sky, coincides with the vernal equinox, an event that can occur at any time during the 24-hour diurnal period. The vernal and autumnal equinoxes are defined as the points of intersection between the ecliptic (the apparent path of the Sun on the sky) and the celestial equator (the projection of the equator of the Earth on the sky), although the vernal equinox is the reference point from which the right ascensions (equator system) and the longitudes (ecliptic system) of the heavenly bodies are measured (Note 3). The vernal equinox is also the moment when the Sun appears to cross the celestial equator heading northward. However, nowadays it is more conveniently defined as the instant when the Sun's ecliptic longitude is zero degrees. The Nowruz event is at present measured to an accuracy of better than 1 millisecond (Malakpour 2004). Using the ephemeris calculated by the French Institut de Mécanique Céleste et de Calcul des Ephémérides (IMCCE) for the Gregorian interval A.D. 1583-2500, we find that 584 equinoxes, or about 64% of the whole events, occur on March 20 for the Tehran longitude. The distribution among the neighboring dates is presented in Table 1. Each year the vernal equinox occurs later, with a delay usually under 6 h, with respect to the preceding one. The delay is equal to the fraction of the day which exceeds the year of 365 entire days. The date of the vernal equinox does not follow this systematic forward shift because the accumulated delays are absorbed in the Iranian calendar by the leap day added to the calendar every four or five years (see below, Section 5).
The IMCCE data allowed us also to calculate the shift dt = t(n+1) - t(n) for the interval +1000 to +2500, t being the instant of the vernal equinox for year n. This resulted in the average value of 5.81662 h ± 0.00240 (standard deviation) or 5h 48m 59.83s ± 8s (s.d.), for the interval A.D. 1000-2500. The lower and upper bounds, 5.54111 and 6.06444 h belong to years 1095 (A.P. 474) and 1216 (A.P. 595) respectively. The plot showing the variation of the delay, dt, over the years is displayed in Figure 1. Since the length of the vernal-equinox year is not constant (see below, Section 3), the average shift depends on the interval considered. Table 2 shows the shift for several different intervals, as well as the corresponding average year length referred to two successive vernal equinoxes, in real solar time.
Table 1. Iranian equinox dates for
period A.D. 1583-2500March date Event frequency Percentage (%) 18 0 0 19 33 3.6 20 584 63.6 21 301 32.8 22 0 0
Obviously, the first day of the calendar year cannot start at the precise time of the vernal equinox and should begin at midnight (Tehran true time), the beginning of the day according to a long Iranian tradition (Note 4). Consequently, if the vernal equinox falls before noon on a particular day, then that day is the first day of the year. If the vernal equinox occurs after noon, the following day begins the calendar year. In other words, the year begins at the midnight closest to the instant of equinox. In the past this was achieved by observing noon altitudes of the Sun and declaring Nowruz to be the day when the solar altitude first exceeded the altitude of the celestial equator. Although the calendar year can start with a delay or advance of less than 12 h with respect to the equinox event, the exact instant of the vernal equinox, or the year transition (tahvil-e sâl), has utmost cultural importance. No matter the moment during day or night, all family members, cleansed and dressed in new garments, wait the astronomical occurrence around a ceremonial table (haft-sin) decorated with several symbolic items. Nowadays the instant of Nowruz is aired by TV and radio stations, whereas in the past canon shots or wind instruments and drums were used to mark the event. When the exact time arrives, there is a burst of rejoicing and cheering and greetings are exchanged.
Table 2. Average time delay between two successive vernal equinoxes Epoch interval Shift
(hour)
(h, m, s)Average year
(solar days)-4000 to +2500 5.81458
5h 48m 52.5s365.242274 0 to +2500 5.81603
5h 48m 57.7s365.242335 +1000 to +2500 5.81662
5h 48m 59.8s365.242359 +1500 to +2500 5.81669
5h 49m 0.1s365.242362 +1800 to +2200 5.81537
5h 48m 55.3s365.242307 +800 to +1200 5.81609
5h 48m 57.9s365.242337 +1995 to +2005 5.83087
5h 49m 51.1s365.242953
The starting point of the current Iranian calendar is the vernal equinox occurred on Friday March 22 of the year A.D. 622 (Note 5). Historically, on 22 September of that year (7th of the Arabic month Rabi' I), the Islam's prophet emigrated to Medina (Hijra). However, the second Caliph Umar ibn al-Khatab, when adopting a calendar system around A.D. 638, preferred to take the starting point of the Islamic lunar calendar two months and eight days back, at the beginning of the Arab sacred month of Moharram, corresponding to July 19, A.D. 622. On the other hand, the fact that in the lunar calendar the months are not related to the natural seasons and the dates move with respect to the solar cycle makes the lunar calendar inadequate for the civil administration (for example for agriculture scheduling and harvest-tax collection). Therefore, the troubles brought by the lunar calendar were strongly felt in Iran four centuries later during the reign of Jalâl ad-Din Malek Shâh, of the the Saljuqid dynasty. Moreover, the Nowruz celebration had slipped into the middle of the Pisces sign, due to neglecting the intercalations (see below, Section 5), and in fact, according to early historians and astronomers, the main purpose of the reform was to fix Nowruz at the vernal equinox (Encyclopedia Iranica).
For the reasons mentioned above, the brilliant vizier and political figure Nezâm-ol-Molk persuaded Malek Shâh to reform the calendar. He appointed a group of astronomers headed by Omar Khayyâm (Note 6) who organized an astronomical observatory in the capital city Isfahan (some sources have mentioned Rey or Neyshâpur). On the basis of observations and calculations, the reform panel adopted the vernal equinox of the year A.D. 622, which places the beginning of the Iranian calendar six months before the Hijra. Similarly, it invented a unique intercalation system based on a 33-year cycle, which will be described below (Section 5). Furthermore, the reform panel adopted 12 equal months of 30 days each, and inserted the remaining 5 or 6 "stolen days" or andargâh (epagomena) between 30 Spandarmad (Esfand) and Nowruz, as was practiced in the Iranian pre-Islamic calendar. And, interestingly, the panel revived the ancient Persian month names (Table 3), although other alternatives were considered and new Persian poetic names were proposed.
Table 3. Iranian calendar months and seasons Order Avestan
(A.D. c. -2000 to -300)Middle Persian
(A.D. c. -300 to +700)Modern Persian Days Seasons 1 Fravashi/Fravarti
[Divine essence]Frawardîn Farvardin 31 Spring 2 Asha Vahishta
[Best righteousness]Ardawahisht Ordibehesht 31 Spring 3 Haurvatât
[Wholeness, integrity]Khordâd Khordâd 31 Spring 4 Tishtrya
[Sirius, rain star]Tîr Tir 31 Summer 5 Amérétâ
[Immortality]Amurdâd Mordâd/Amordâd 31 Summer 6 Khshathra Vairya
[The good dominion of choice]Shahrewar Shahrivar 31 Summer 7 Mithra
[Sun, friendship, promise]Mihr Mehr 30 Autumn 8 Ap
[Water]Âbân Âbân 30 Autumn 9 Âthra
[Fire]Âdur Âzar 30 Autumn 10 Dathushô
[Creator]Day Dey 30 Winter 11 Vohu Manah
[Good Mind]Wahman Bahman 30 Winter 12 Spéntâ Ârmaiti
[Holy serenity]Spandarmad Esfand 29/30 Winter
We notice therefore that the reform's objective was not only resolving administrative and economical problems, but also aimed at preserving Nowruz, one of the main symbols of the Iranian identity. In brief, the reform had an outstanding consequence, probably unprecedented in the Iranian history. It attached Nowruz tightly to the vernal equinox, which was not the case in the Sasanian Zoroastrian calendar, because the latter did not apparently employ the 4-year intercalations, but instead added a supplementary month to the calendar every 120 years (de Blois 1996).
In contrast to the Islamic calendar, which is based on the lunar synodic month and the corresponding lunar year of of 354 days, the Iranian year is divided into 12 months with tight links to the real, annual seasons. The first 6 months of the modern calendar have 31 days, the next 5 months 30 days and the last one 29 or 30 days. This scheme of month lengths is in accord with the fact that the astronomical seasons do not have an equal number of days, spring and summer being longer than autumn and winter (Note 7). The month names, in their original Avestan form (Note 8), their meanings, and their linguistic evolution over the ages are presented in Table 3.
3. The length of the year
The Iranian year is a "tropical year" with the vernal equinox as its reference point. However, it should not be confounded with the tropical year set up by modern astronomers (Note 9). Nowadays, the tropical year is defined as the interval during which the Sun's mean longitude, referred to the mean equinox of the date, increases by 360 degrees. This definition was adopted by the International Astronomical Union at its General Assembly in Dublin in September 1955 (Seidelmann et al. 1992). Several researchers, notably Meeus & Savoie (1992), Cassidy (1996), and Meeus (2002) have underlined the difference between the vernal-equinox year and the newly introduced tropical year. Nonetheless, the mistake of equating the two is unfortunately largely propagated. In fact most astronomers and calendar adepts are defining the tropical year as starting with the vernal equinox but using the length of the newly-defined tropical year for their calculations (Note 10). And unfortunately some Iranian astronomers and calendar experts are not exempt from this confusion.
It should be emphasized that this new concept of the tropical year, introduced for celestial mechanical studies, is based on the mean longitude of the Sun and does not depend on a specific origin for the annual apparent motion of the Sun. It aims at the long-term behavior of the year by taking into account the precession (secular terms) and not short-term, periodic gravitational disturbances. No matter how useful this concept, the traditional solar calendars, Iranian as well as Gregorian (Note 11), are based on the mean length of the real vernal-equinox year. The situation of the nomenclature as it is now lends itself to confusion, because the same term (tropical year) is used for two different, but very closely related, concepts. Therefore, it would be highly expedient for the International Astronomical Union to remove the ambiguity by adopting two distinct terms for both notions. It would be quite logical to apply "tropical year" only in its modern, celestial mechanical meaning, and use the term "vernal-equinox year" for the interval between two successive passages of the Sun through the vernal equinox. Naturally, Iranians call it the Nowruz year.
Let us look more closely into the difference between the tropical and vernal-equinox years. Bretagnon and Rocher (2001) give the following expression for the length of the tropical year:
365.24219052 - 61.56 10-6 T - 68.4 10-9 T2 + 263.0 10-9 T3 + 3.2 10-9 T4 [1]
where T is the barycentric dynamical time (TDB) or, more simply, uniform (ephemeris) days of 86400 seconds (International Atomic Time, TAI), counted in Julian millennia (of 365250 days) from the present epoch. The expression is valid over an interval of ±10,000 years from J2000.0. Expressed in universal time, based on the Earth's rotation about its axis, the same authors give the following polynomial formula for the tropical year:
365.2421789 - 135.63 10-6 T - 68.4 10-9 T2 + 263.0 10-9 T3 + 3.2 10-9 T4 [2]
where T here is universal time. We see therefore that at the epoch of J2000 the length of the tropical year was 365.24219052 uniform days of 86400 seconds, which is equal to 365.2421789 real solar days, and can be rounded off to 365.2422 days. The formulas [1] and [2] also indicate that the length of the tropical year is not constant. As shown also in Figure 2, it is decreasing by about 5 milliseconds per year, because the precession is presently speeding up. In addition, not shown in Figure 2, its length in real solar days decreases by about another 6 millisecond per year as a result of the slowing down of the Earth's rotation about its own axis, mainly due to the tidal effect of the Moon. It should be underlined that presently we are unable to accurately predict the length of the day. The reason is that the Earth's rotation undergoes unpredictable, irregular variations over different time scales, as a result of both internal and external geophysical processes and astronomical perturbations.On the other hand, the mean time interval between two successive vernal equinoxes, as derived by Meeus (2002) for the true longitude of the Sun, based on the orbital elements of the Earth (Simon et al. 1994) and the exact solution of Kepler's equation, is represented by the polynomial expression:
365.2423748 + 10.34 10-5 T - 12.43 10-6 T2 - 22.63 10-7 T3 + 1.31 10-7 T4 [3]
for the period ranging from about 500 B.C. to A.D. 4500, where T is measured in Julian millennia of 365250 (ephemeris) uniform days from the epoch J2000.0. It should be underlined that this expression represents the global evolution of the real vernal-equinox year over large time-spans by allowing for the non-uniform Keplerian motion of the Earth. It does not, however, take into account the fluctuations in the length of the year caused by various periodic gravitational perturbations. The exact solution is obtained in the IMCCE ephemeris by an equation composed of 96 terms. The above equation [3] can be expressed in solar days, as:
365.2423632 + 2.93 10-5 T - 12.43 10-6 T2 - 22.63 10 -7 T3 + 1.31 10-7 T4 [4]
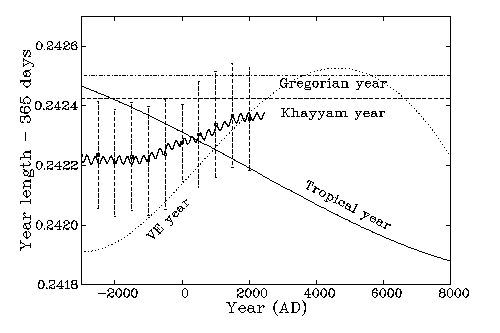
The comparison between equations [3] and [1] or [4] and [2] shows clearly that the mean vernal-equinox and tropical years do not have the same length. For example, for the epoch of +2000, the mean tropical year is 365.2421789 days, whereas the mean vernal-equinox year is 365.242362 days, that is 15.82 s longer. In the same way that the tropical year was rounded off to 365.2422 days, the vernal-equinox year can be approximated to 365.2424 days. Moreover, it is obvious from equation [3] that the vernal-equinox year also varies over the ages (see also Figure 2). Around the epoch -3000 it was 365.241872 uniform days, whereas and at the beginning of the Christian era it was increasing to 365.242138 uniform days. It is still increasing and will attain its largest value, 365.242525 uniform days, in the epoch +5000. Therefore, the difference between the vernal-equinox and tropical years is not limited only to their lengths, since their long-term variations over the time are also dissimilar. In contrast to the vernal-equinox year, the tropical year will continually decrease at least until the epoch +8000.
Figure 2 also displays the variation of the real vernal-equinox year, in solar days, obtained by the IMCCE calculations. Those data are shown in two different forms for the sake of better visibility, since the year exhibits considerable fluctuations over relatively short periods. The discrete points, centered on vertical bars, represent a mean value for a 500-year interval with the bars showing the standard deviation over that interval. The smallest range of the fluctuations belongs to the epoch 0 where the vernal-equinox varies over about 20s, while for the epoch +2000 the spread is twice larger. The undulating curve displays the IMCCE data after being smoothed out by a filtering method in which all the variations with periods under 100 years are removed. We see therefore that the main fluctuations in the length of the vernal-equinox year result from relatively short-period perturbations. The overall shape of the real vernal-equinox year nears that of the mean vernal-equinox year if we use a stronger smoothing technique. Note that in order to convert uniform days into solar days one must use a correction parameter, called the derivative of Delta-T, which can be represented by the difference between equations [1] and [2]. Generally, the correction increases the uniform-day years before the epoch +2000.0 and reduces those after that epoch (Note 12).
As it was pointed out above, the length of the real vernal-equinox year can deviate considerably from the mean value over short periods mainly due to the gravitational pull of the Moon and the planets. The fluctuations of the year length are also visible in Figure 1. Over the interval A.D. 1000-2500 the shortest year, 365.230880 days, is A.D. 1095 and the longest A.D. 1216 with 365.252685 days, or 365d 6h 3m 52.0s. The mean length depends on the interval considered, as displayed in Table 2. We see that around Khayyâm's epoch the mean duration of the vernal-equinox year over the 400 year interval A.D. 800-1200 was 365.242337 solar days, which is also the average value for the whole period 0 to +2500. In the following we will use a mean value of 365.242362 days (corresponding to the period +1500 to +2500) for the length of the vernal-equinox year in the coming centuries.
4. The difference between the "tropical" and Iranian years
Here we give more explanations in order to highlight the fact that the Iranian vernal-equinox year is not equal to the newly introduced "tropical year". Since the Earth's orbit around the Sun is elliptical, its orbital velocity is not uniform. At the perihelion of its orbit the Earth is the closest to the Sun, and therefore moves faster than average, while at aphelion, when it is the farthest away from the Sun, it moves slower. Moreover, due to the precession, the vernal equinox slowly regresses along the ecliptic by 50.3 arcseconds per year with respect to stars, while the major axis of the Earth's orbit rotates in the direct sense by 11.6 arcseconds per year. Consequently, when the Sun crosses the vernal-equinox point, spending a year in its apparent path along the ecliptic, the Earth has not made a complete circuit. It has made a complete journey on a distorted orbit (due to the rotation of the orbit) less a small arc. This small arc is covered with a somewhat different speed, according to its position with respect to the perihelion of the Earth's orbit. As a result, depending on the starting point adopted for the "year", one complete circuit in tropical longitude will have a somewhat variable length. This means that the length of a "real" tropical year depends upon the chosen reference point on the ecliptic.
A simple mathematical formula can facilitate the explanation. The year length can be represented by: Y = T - t, where T is the time needed by the Sun for making a complete circuit with respect to the perihelion and t the time gained because the reference point approaches the Sun. The time gained is represented by the ratio of the arc length, S, and the apparent velocity of the Sun: t = S/V. But since the arc length is constant, t depends only on the velocity. For example, at the December solstice the Earth is near the perihelion (to which it arrives in early January) and the Sun apparently moves faster than average towards the solstitial point. Hence the time gained is smaller than that for the vernal equinox, and the tropical year as measured for this point will not only be longer than that for the vernal equinox, but the longest of the four cardinal years. On the basis of the planetary ephemeris calculated by Simon et al. (1994), Meeus (2002) has derived the mean intervals between two successive passages of the Sun through the four seasonal points for several epochs. The results, listed in Table 4, clearly show that these various "tropical" years do not have the same length (Note 13). And, more particularly, the vernal-equinox year is different from the "tropical" year. In fact the "tropical" year represents the mean value of the four seasonal figures (Note 14). It should be emphasized that the year lengths listed in Table 4 are in uniform days, and must be converted into solar days for calendar use, as listed in the second row for the vernal-equinox year (Note 12).
Table 4. Various "tropical" years for several epochs *
Epoch Vernal-equinox
Nowruz yearSummer-solstice
yearAutumnal-equinox
yearWinter-solstice
year-1000 365.242022
365.24223365.241859 365.242718 365.242871 0 365.242138
365.24227365.241726 365.242496 365.242883 +1000 365.242261
365.24232365.241648 365.242257 365.242840 +2000 365.242375
365.24236365.241627 365.242018 365.242741 +3000 365.242464
365.24237365.241659 365.241800 365.242594 +4000 365.242516
365.24235365.241734 365.241620 365.242407 * The year lengths are in ephemeris (uniform) days, except for the vernal-equinox year which is given also in real solar days.
The length of the year in the Iranian calendar, as conceived by Khayyâm et al., is 365.2424.. days (Youschkevitch & Rosenfeld 1973), a logical consequence of the intercalation system: 365 + 8 / 33 = 365.2424.. (see Section 5). This is in good agreement with the length of the year at his time, 365.2423 days. Khayyâm's estimate of the year length agrees even better with the present-day mean value of 365.2424 days. Compared to the Gregorian year of 365 + 1 / 4 - 1 / 100 + 1 / 400 = 365 + 97 / 400 = 365.2425 days, Khayyâm's value was based on a more accurate knowledge of the solar annual motion. Note that recently an extremely precise value for the duration of the year (365.24219858156 days) has been attributed to Khayyâm (O'Connor & Robertson 1999), although it is supported by no historical source, as far as we know. We think that this may be a spurious value resulting from the erroneous 2820-year cycle suggested recently (see below Section 7).
The precise knowledge of the year duration is one thing, using it practically to construct a calendar system is another, because the calendar year of 365 entire days is not equal to the real solar year. A good calendar is therefore the one whose intercalation system yields a year length the nearest possible to the reality.
5. The intercalation system
The average time shift, dt, between two successive vernal equinoxes, listed in Table 2, indicates also the excess time with respect to a calendar year of 365 full days. In other words, each year the solar time leads by dt/24 day with respect to the calendar. Taking dt = 5.81662 h for the interval +1000 to +2500, this lead will be 5.81662/24 = 0.242359 ≅ 0.2424 days per year. Thus, after four years, the advance amounts to 4 x 0.24236 = 0.96944 days, which is approximated to 1 day, necessitating a leap year of 366 days. This correction of 1 day every 4 years is though too generous and therefore results in a lead of the calendar year over the solar year. This point constitutes the fundamental problem of the solar calendars, and this is the reason why in the Iranian calendar the intercalation is not carried out systematically every 4 years (see below). On the other hand, if no intercalations are applied, the Nowruz feast will regress with respect to the vernal equinox, moving through all the seasons in about 1506 years. More explicitly, after four years the vernal equinox will happen on Farvardin 2 and after eight years on Farvardin 3, and so on. At the same time, Nowruz will slip more and more into winter.
The Iranian calendar has a basic, 33-year intercalation cycle, which consists of 33 x 0.2424 = 7.9992 = 8 leap years of 366 days and 25 ordinary years of 365 days. There are two kinds of leap years: i) leap year after 3 ordinary years (called quadrennial), ii) leap year after 4 ordinary years (quinquennial). During a quadrennial period, the vernal equinox occurs as two pairs systematically two times after noon then two times before noon. However, about every 33 years a vernal equinox happens very close to midnight, coming between two such pairs and forming a quinquennial period. More explicitly, this situation happens dominantly every 33 years and sometimes, much less often, after an interval of 29 years.
The first leap year of the 33-year cycle is quinquennial and the seven others quadrennial. The intercalations are therefore applied to the years: 5, 9, 13, 17, 21, 25, 29, 33. The total cycle amounts to 25 x 365 + 8 x 366 = 12053 calendar days. In comparison, the solar time duration is currently 33 x 365.242362 = 12052.99795 days. This means that a 33-year cycle advances by 0.00205 days, or about 3 minutes, with respect to the solar time. This is the reason why a strict 33-year cycle needs future adjustments. Assuming a constant length for the vernal-equinox year, after about 500 cycles, or about 16,000 years, the advance will add up to 1 day. However, since the duration of the year decreases after the epoch +3000 and would reach a value of about 365.24182 days in the epoch +8000, a shorter period is required in order that the advance attain one full day. Anyhow, when the error totals 1/33 of a day, a 33-year cycle needs to be shortened to 29 years in order to keep the calendar in pace with the solar time. It should be emphasized that detailed extrapolations over very long periods are unavailing because the year length is not constant and moreover unknown perturbations may add up in the distant future to have a considerable effect.
In the past, when Newton had not yet put forward his theory of gravitation and Laplace, Lagrange, Euler, Hamilton, and others had not contributed to the formulation of celestial mechanics, the precise instant of the vernal equinox was predicted by extrapolating detailed observations. Today, thanks to the remarkable improvements in the models of orbiting bodies, and more particularly the development of powerful computers and numerical methods, the instant of the vernal equinox can be predicted with very high precision. However, observational measurements are necessary to check the actual correspondence between the mathematical model and the reality. The observations are also an important part of the Iranian calendar culture, and it would be wise to be preserved. Moreover, now that amateur astronomy has made big technical advances, more people can participate in the observation of the solar motion around Nowruz. Since Nowruz is accompanied by several public ceremonies and festivities, the widespread observation of the Sun around the spring equinox can be a delightful modern addition. This will also provide a good opportunity for teaching astronomy and calendar science to the public. The same thing can be recommended also for the observation of the solar motion during the Mehregân festival at the beginning of Mehr, the 7th month, which celebrates the autumnal equinox (Notes 15 & 16).
6. A notice of historical interest
The information about Khayyâm's calendar reform come to us not directly from himself, but only through brief accounts by later astronomers. In fact 13 years after the instauration of the reform Khayyâm fell into disgrace after Malek Shâh's death and Nezâm-ol-Molk's murder by Assassins, a politico-religious order led by Hasan Sabbâh. Following the death of the king, his wife ruled as regent for two years, and Khayyâm fell heir to some of the hostility she had demonstrated towards his patron, Nezâm-ol-Molk, with whom she had quarreled over the question of royal succession. Moreover, orthodox Muslims, who disliked Khayyâm because of his freethinking, evident in his quatrains, became highly influential at court. Maybe they were not happy neither with Khayyâm's frank moves for valuing the Persian identity. Financial support was cut from the observatory and its activities, among which the reform, came to a halt (Youschkevitch & Rosenfeld 1973).
There is no doubt though that Khayyâm and his group implemented the intercalation system based on quadrennial and quinquennial leap years. The astronomer Khâzeni (Note 6), who was probably a member of the reform group and later, during the reign of Sanjar, Malek Shâh's son, authored the Sanjari zij (astronomical observations and tables), uses the quadrennial/quinquennial intercalations, which most probably resulted from the work done by Khayyâm's reform group. For a period of 220 years in the Jalâli calendar, Khâzeni calculates 53 intercalations, 8 quinquennial and 45 quadrennial (Note 17). About two centuries later, the eminent astronomer and mathematician Nasireddin Tusi (A.D. 1201-1274), director of Marâgha observatory who created the Ilkhani zij, and is recognized for having made an exhaustive criticism of Ptolemic astronomy and having presented a new mathematical model of planetary motions, gives brief but important information about the Jalâli reform. In his Ilkhani zij, he clearly states that an intercalation is applied every 4 years, making a year of 366 days, and after 7 or 8 quadrennial intercalations a quinquennial intercalation is performed on the basis of induction. We see therefore an implicit reference to the scheme of 29 or 33-year cycles. For information about the various intercalation attempts over centuries, based on the quadrennial/quinquennial design, see Sayyâd (1981) and the recent interesting work by Abdollâhi (1996), which deals with the whole history of the Iranian calendar.
7. The putative 2820-year cycle
Recently some Iranian calendar experts, mainly the late Behruz (1952) and the late Birashk (1993), have suggested the existence of so far unknown cycles in the Iranian calendar. In particular, they divide the calendar into cycles of 2820 years, itself split in 21 subcycles of 128 years and 1 subcycle of 132 years (2820 = 21 x 128 + 132). The subcycles of 128 and 132 years are themselves divided into periods of 29, 33, and 37 years (128 = 29 + 3 x 33; 132 = 29 + 2 x 33 + 37). In brief, the cycle consists of 2137 ordinary years and 683 leap years.
This scheme contains several drawbacks. It is claimed that the 2820-year cycle represents the interval after which the vernal equinoxes are repeated at the same instant of the day. The scrutiny of the IMCCE ephemeris data does not allow us to uphold this claim, which has already been criticized by calendar researchers, among them the Iranian astronomers Malakpour (2004) and Sayyâd (2000). Moreover, the whole 2820-year cycle gets a lead of about 0.5 days over the solar time. Using the present length of the vernal-equinox year, the cycle amounts to 2820 x 365.242362 = 1029983.461 days, while the calendar will have 2137 x 365 + 683 x 366 = 1029983 days. In order that the cycle remain in step with the solar time, the year length must therefore be 365.2421986 days or about 365.2422 days. This figure, which results also from the fraction 683/2820, seems to be the length of the modern tropical year, mistaken for the duration of the vernal-equinox year. As a result, the scheme runs into trouble many times during a period of 2025 years, for example 21 March A.D. -1, 21 March A.D. 1600, and 21 March A.D. 2025.
The 2820-year cycle may be at the origin of the extremely precise duration of the year (365.24219858156 days) attributed to Khayyâm (see above, Section 4). In fact, the fraction 683/2820 implies a year of 365.2421985815603 days, which surprisingly resembles the attributed value, thus casting doubt on its authenticity. This spurious value may stem from the mistake that Khayyâm was the author of the 2820-year cycle. However, there is no historical record relating that cycle to Khayyâm (Sayyâd 2000). The confusion is probably due to the fact that Behruz (1952) proposed his scheme in the form of tables which he called "Khayyâmic tables", leaving so the door open to misinterpretation.
The conception of such a cycle seems therefore to result from a confusion between the vernal-equinox and tropical years, as explained above, and moreover does not take into account the secular variation of the year length. Furthermore, this complex system does not make the calendar more precise, since the presently followed 33-year scheme, although much simpler, is quite efficient.
8. Correspondence with other calendars
There are several reliable software codes for converting the Iranian calendar dates and week days into other calendar systems and vice-versa. We can mention the "Khayam" Program:
http://payvand.com/calendar
set up by Hossein Bâgher-Zâdeh for the correspondence between the Iranian and Gregorian calendars. Currently the leap years in the 33-year cycles are those years that after dividing by 33 leave a remainder of 1, 5, 9, 13, 17, 22, 26 and 30. For example, the year A.P. 1375 that begun on March 20, 1996 has the remainder of 22 and thus is the leap year. These rules are implemented in the "Khayam program". In a recent paper Borkowski (1996/1997) argues that the algorithm employed in that program is valid for the years A.D. 1799 to 2256 (A.P. 1178 to 1634). Moreover he presents a concise code which reconstructs the pattern of leap years over a time span of about 3000 years.
Another interesting tool is the Calendrica 2.0 software package, based on the algorithms in Calendrical Calculations: The millennium Edition, by Edward M. Reingold & Nachum Dershowitz. The online version:
http://emr.cs.iit.edu/home/reingold/calendar-book/Calendrica.html
allows conversion not only between the Iranian and Gregorian systems, but also among several other calendars, mainly: Armenian, Chinese, French revolutionary (Note 18), Hebrew, Hindu, Islamic, Mayan, and the mistaken arithmetic version of the Iranian calendar programmed with the 2820-year cycle of intercalations.
9. Remarks on the ancient origin of the Iranian calendar
The first Iranian states were founded by the Medes (728-550 B.C.) and the Achaemenids (550-330 B.C.). We have a number of information about the calendars used during the Achaemenid period, but documents pertaining to the pre-Achaemenid history of Iran are not only scarce but also silent on the calendar during that period.
Several historical and archeological clues point to a lunisolar administrative calendar during the Achaemenid era, probably borrowed from the Babylonians. At the same time, there was a solar calendar widely used by Iranians. The reason for adopting the Babylonian calendar was certainly political. The Achaemenids (Cyrus the Great himself?) wanted to use the Babylonian administrative system, for they had more experience than the Persians. Adopting this calendar was also a sign of respect toward one of the peoples making up the Achaemenid empire. Similarly, Cyrus the Great paid official respect to Marduk, the supreme Babylonian god during his coronation ceremony. Abdollâhi (1996) gives several convincing arguments in support of the Babylonian influence, while he firmly refutes the opinion forwarded by several workers that the Achaemenid state calendar followed an Egyptian model.
Briant, a specialist of the Achaemenid era, referring to ancient authors (Plutarch, Diodorus, Quintus Curtius, Dicearchus), believes that there existed a solar calendar of 360 days and 5 epagomenal days, along with the state lunar type Babylonian calendar. Another historical fact corroborates the existence of an ancient solar calendar among Iranians during that period. We know with certainty that the Zoroastrian solar calendar was taken up by Cappadocians after the conquest of Asia Minor by Cyrus the Great who entered in Sardes in 546 B.C. The Cappadocian solar calendar, with 12 months of 30 days plus 5 epagomenal days, was an imitation of the Zoroastrian calendar as is made especially blatant by the names of Iranian months and their order (Encyclopedia Iranica). Let us not forget that after Asia Minor came under Persian rule many Iranians settled in that region where, among other things, they set up Zoroastrian fire temples. We note also that in the 4th century A.D., that is some 700 years after Alexander's conquest, many villages in Cappadocia were inhabited by the Iranians descendants of the first colons. The fact that during the Achaemenid domination the Cappadocians borrowed the Zoroastrian calendar and not the official state calendar points to the deep roots of this calendar among Iranians, in particular as far as the everyday cultural and religious matters were concerned. And this implies that the Zoroastrian calendar was more ancient than the official adoption.
The historical documents as to the Iranian calendar in ancient times are so few that no information should be overlooked. The explanations supplied by Biruni are of paramount importance (de Bloy 1996). In fact, Biruni has provided several information about the Iranian pre-Islamic calendar, and they have proved to be exact (Abdollâhi 1996). Biruni, in his Athar al-baqia, tells us about the calendar used by the Pishdadis, the earliest Iranian dynasty according to the traditional history. Their first king was the mythological Kiumars. The Pishdadis are followed by the Kiyanis, whose last king Dârâ (Darius III) was killed during Alexander's conquest of Iran. Since Biruni similarly counts Kourosh (Cyrus) and Ardashir (Artaxerxes I Longimanus) among the Kiyanis, and identifies the Kianis with the Achaemenids, the Pishdadis are more ancient than the Achaemenids. And according to legends, Nowruz was established by the Pishdadi king Jamshid (Yima/Yama in the Indo-Iranian lore) whose time goes back to the beginning of Indo-Iranian settling process and transition from hunting to animal husbandry, a very ancient time in which apparently happened a glaciation. Anyhow, these legends underline the great ancientness of Nowruz as well as its cultural importance.
According to Biruni, the Pishdadis counted 360 days in a year and 30 days in a month. They carried out a leap month every 6 years and called it a leap year. Then every 120 years they performed two leap months, one for the 5 uncounted days and the other for the overlooked quarters of a day. The year length in that calendar can be calculated as follows (Abdollâhi 1996):
one year = 12 x 30 = 360 days,
6 years = 6 x 360 + 30 = 2190 days,
120 years = 20 x 2190 + 30 = 43830 days,
43830/120 = 365.25 days,
that is 365 days and a quarter of the day. Obviously, this is possible in a solar calendar only. Therefore, if we believe Biruni, the pre-Achaemenid Iranians used a solar calendar. Moreover, the above specifications point to a Zoroastrian calendar. This implies that, contrary to a prejudice, the Egyptians were not the sole among ancient civilizations to use a solar calendar. We do not know when that calendar started, even if according to Biruni Zoroaster himself introduced the month intercalation. Although we do not know exactly when Zoroaster lived (certain Greek sources have placed him in 6000 B.C., whereas the tradition associates him with 600 B.C.), recent studies concerning the linguistic particularities of the Gathas (the oldest part of the Avesta, attributed to Zoroaster himself) suggest around 1500 B.C. for his time (Encyclopedia Iranica).
At some point the Iranian calendar was reformed: instead of observing a full month intercalation every 6 years, the lacking 5 days, called andargâh, were inserted after the 360th day. The date on which the 365-day system was created is a matter of debate. W.E. West proposed 505 B.C., Markwart put it in 493-90, Boyce initially suggested the Sasanian period, but has recently revised her initial estimate to the Achaemenid era (Encyclopedia Iranica). But the question remains open.
The prominent feature of the Iranian calendar is Nowruz, which in the Zoroastrian belief is associated with fire, the seventh creation of Ahura Mazda. Nowruz is in fact the most important festival in the Zoroastrian solar calendar. According to Boyce (op cit. under Gâhanbârs), among the seven very ancient Zoroastrian festivals, ``only Nowruz appears to have real doctrinal justification, since the ``new day'' was celebrated at the spring equinox, when the Sun, the most powerful representative of the creation of fire, is giving renewed warmth and life to the world. ... It seems highly probable that Nowruz, with its profound theological symbolic significance, was established by Zoroaster himself.''
10. Conclusions
In this paper, we presented a detailed description of the Iranian calendar emphasizing the underlying astronomical phenomena, without ignoring the related historical topics. A prominent feature of the Iranian year is its starting point, Nowruz, which coincides with an astronomical event: the Sun's arrival at the vernal equinox. Nowruz, which symbolizes the rebirth of the nature and the triumph of life over the oppressive cold and darkness of the winter, is celebrated by a large number of peoples in the Western and Central Asia.
On the basis of the ephemeris provided by the French IMCCE for the period A.D. -4000 to +2500, and the equations obtained by Bretagnon & Rocher (2001) and Meeus (2002), we discussed the various definitions of the year and showed that the Iranian calendar is based upon the vernal-equinox year and not on the "tropical" year.
In fact the modern concept of the "tropical" year, formulated by researchers in the field of celestial mechanics, represents a mean year which does not depend on a particular starting point on the ecliptic. Moreover, it leaves out short-term fluctuations in the duration of the year.
Therefore, the "tropical" year of 365.2422 days does not at all correspond to the interval between two successive passages of the Sun through the vernal equinox. Attributing the value of 365.2422 days to such time interval is a mistake, unfortunately widely propagated.
In contrast, the Iranian, or real vernal-equinox, year relies on the Keplerian, non-uniform motion of the Earth around the Sun as well as on the short-term perturbations. This is why successive observations of the Sun's passage through the vernal-equinox are necessary in order to determine the starting instant of the new year and the real duration of the previous one.
Neglecting the short-term fluctuations, the mean length of the Iranian, or vernal-equinox, year at the present epoch is 365.2424 solar days. This time length represents the mean interval between two successive passages of the Sun through the vernal equinox.
The difference between the "tropical" and vernal-equinox years though is not limited to their length since their long-term variations is also unalike.
The confusion between both concepts is not only scientifically wrong, it may entail other mistakes and can also undermine the accuracy of the Iranian calendar. However, since the importance of this issue is often not appreciated even among calendar experts and astronomers, in order to avoid the mistake, we proposed using two distinctive terms, "tropical year" for the newly introduced concept and "vernal-equinox year" when solar calendars, Iranian or Gregorian, are concerned.
The length of the year, as laid down by the intercalation system adopted by the Khayyâm reform, is 365.2424.. days. This estimate agrees well with the real vernal-equinox year at Khayyâm's epoch, which had a mean value of 365.2423 days, and is even in better agreement with the current length of the vernal-equinox year, whose mean value is 365.2424 days.
We also analyzed the unparalleled intercalation system of the Iranian calendar, which is based on a 33-year cycle, and pointed out the astronomical foundation of this cycle. There are two types of leap years in the Iranian calendar, quinquennial and quadrennial. The cycle contains 8 leap years, the first one being quinquennial and the seven others quadrennial.
Finally, we explained why the recently proposed 2820-year cycle is fallacious, and argued that most probably it is due to a confusion between the vernal-equinox and "tropical" years. This cycle is not only erroneous, but also such a complex intercalation scheme seems useless for the Iranian calendar, since the 33-year cycle is almost perfect. We argued also that this scheme is at the origin of the extremely precise length of the solar year attributed to Khayyâm.
Acknowledgements. It is a pleasure to thank the French Institut de Mécanique Céleste et de Calcul des Ephémérides (IMCCE), Director Dr. William Thuillot, and Dr. Patrick Rocher for providing the ephemeris which was essential for this study and also for helpful discussions. My field of research in astrophysics being well outside that of calendars and time reckoning, I learned a lot in the process of writing this paper and would like to thank all the people who took part in this project. I am particularly indebted to the calendar expert Mr. Simon Cassidy, Emeryville Ca. U.S.A., for numerous e-mail exchanges and for a critical reading of the paper which contributed to improve its content. I express my deep gratitude to him. I benefited also from discussions and comments by several colleagues at Paris Observatory, in particular Dr. Thibaut Le Bertre, Dr. Jean-François Lestrade, and Dr. James Lequeux. I would like to thank them. I am grateful also to Dr. Vassilis Charmandaris, Cornell University, USA, for comments. My thanks are also directed to Mr. Frédéric Meynadier, Paris Observatory/Paris VI University, for his valuable and efficient cooperation. I am also thankful to Mr. Jean Meeus, Brussels, and Dr. Iraj Malakpour, Geophysics Institute, Tehran, for replying to my questions. I would like also to acknowledge Drs. Edward M. Reingold & Nachum Dershowitz as well as Dr. Hossein Bâgher-Zâdeh for using their calendar conversion codes. I am also grateful to Dr. Kazimierz M. Borkowski, Torun Radio Astronomy Observatory, Nicolaus Copernicus University, Poland, who read the paper and made several interesting comments. I want also to thank Dr. Jafar Âghâyâni-Châvoshi, Sharif University, Tehran, for providing several historical documents. I am also grateful to Dr. M.-Sch. Adib-Soltâni, Tehran, for his remarks, in particular regarding etymology. Finally, I would like to dedicate this paper to the memory of the late scholars Zabih Behruz and Ahmad Birashk, who initiated the modern research on the Iranian calendar.
Notes
1. According to the Gregorian calendar. It corresponds to 15 March in the Julian calendar.
2. Etymology of Nowruz. Modern Persian now "new", Middle Persian nôk, Avestan nava-, Sanskrit nava-, akin to Greek neos, Latin novus, all from the Indo-Eurpean root *newos. The English new, novel, German neu, and French nouveau, neuf belong to this group. The second component, Modern Persian ruz "day", Middle Persian rôc, Old Persian raucah-, Avestan raocah- "light, luminous; daylight", Sanskrit roka- "brightness, light", cognate with Greek leukos "white, clear", Latin lux "light" (also lumen, luna), Indo-Eurpoean root *leuk- "light, brightness". The Persian words rowshan "bright, clear", foruq "light", and afruxtan "to light, kindle" also belong to this family, as well as the English light, German Licht, and French lumière.
3. There is no ambiguity between the vernal and autumnal equinoxes, even if the passage of the Sun through the autumnal equinox is the beginning of spring in the southern hemisphere! The vernal equinox is the point with coordinates 0,0 degree in the ecliptic system, whereas the autumnal equinox is defined by the point 180, 0 degrees.
4. Placing the beginning of the day at midnight is an ancient Iranian practice, as attested by several sources. For example, the famous scientist Abu-Rayhân Biruni (A.D. 973-1048) deals with this matter in his well-known book Athar al-Baqia (ancient history and geography), written around A.D. 1000 (see below, references, for more details). Moreover, he underlines that the Shahriyâr zij, the astronomical calculations and tables established during the reign of the Sasanid emperor Khosrow I Anushiravân around A.D. 555, was based on the adoption of the midnight as the beginning of the day. Note that taking up the midnight for the beginning of the day by astronomers is relatively recent in the Western world. In fact until 1925 astronomers started and ended their days at noon, so the day in Greenwich Mean Time (GMT) originally started and ended at mean solar noon in Greenwich, while Greenwich Civil Time started at midnight. Nevertheless, the Julian days, used by astronomers, begin at noon (GMT).
5. In compliance with the Gregorian calendar. It corresponds to 19 March in the Julian calendar. Taqizâdeh gives 17 March A.D. 622, which is erroneous, as was first pointed out by Birashk.
6. According to various sources, up to eight astronomers participated in the reform project. Apart from Omar Khayyâm, the other recorded names are: Abu-Hâtam Mozaffar Esfazâri, Abd-ol-Rahmân Khâzeni, Meymun ebn-e Najib Vâseti, and Abol-Abbas Lukari. Some historians have brought into question the participation of Khâzeni, a slave-boy of Byzantine origin, owned by Ali ebn-e Khâzen Marwazi, treasurer and chancellor of the court at Marv (now Mary, Turkmenistan), who gave the young man the best possible education in mathematical and philosophical disciplines, so that he became a renowned mathematician/astronomer and "physicist". Khâzeni established a zij for the ruler Sanjar, and invented a balance for measuring specific gravities which was as precise as those obtained up to the Eighteenth or beginning of the Nineteenth century. He passed away in A.D. 1115 or 1130, which is not incompatible with his taking part in the calendar reform. However, the intercalation system he proposes in the Sanjari zij does not fully agree with Khayyâm's scheme (see also Note 17), and this may be interpreted as his non-adherence to the calendar reform.
7. The current lengths of the astronomical seasons, around the year 2000, are about: spring 92.76 days, summer 93.65 days, autumn 89.84 days, and winter 88.99 days. The seasons are unequal because the Earth's orbit is slightly elliptical and the Sun is not exactly at the center of the orbit. As formulated by Kepler's second law, the Earth moves faster when it is close to the Sun than when it is farther away, so the seasons that occur when the Earth is close to the Sun pass more quickly. The Earth reaches its perihelion, the point in its orbit closest to the Sun, in early January and is at aphelion, farthest away from the Sun, in early July. Hence the summer is longer than the winter in the Northern Hemisphere. In the Southern Hemisphere, the winter is longer than the summer.
The present situation is not, however, eternal and the duration of the seasons change through time due to variations in the orbital parameters of the Earth. The precession, or the motion of the orientation of the Earth's rotational axis, changes the positions of the solstices and equinoxes with respect to the perihelion. It takes about 21,000 years (climatic precession) for these points to make a complete circuit along the orbit, with respect to the perihelion. Similarly, variations in the shape, or the eccentricity, of the Earth's orbit (Note 14), which have a periodicity of about 100,000 years, modify the length of the seasons. And finally, changes in the obliquity, or tilt, of the Earth's axis cause important variations in the amount of solar radiation received by the Earth at high latitudes, bringing about considerable alterations in the seasonal climate. The obliquity, which is currently about 23.5 degrees, varies between about 22.5 and 24.5 degrees over a period of approximately 41,000 years.
8. The Avestan, the language of the Avesta, scriptures of Zoroastrianism, belongs to the Iranian group of the Indo-European family of languages. The oldest part of the Avesta, called the Gathas (hymns, songs), made up of poems attributed to Zarathushtra himself, are now commonly thought to date from around the end of the 2nd millennium BC and are thus contemporary with Vedic Sanskrit.
9. A brief etymological note. "Tropical" from "tropic", from L.L. tropicus "of or pertaining to the solstice", from L. tropicus "pertaining to a turn", from Gk. tropikos "of or pertaining to a turn or change, or to the solstice" (as a noun, "the solstice"), from tropos "turn, way, manner, style", tropein "to turn". Indo-European root *trep- "to turn". Other terms of the same origin in English: troubadour, trover, contrive, retrieve, trophy, entropy.
The relation between the notions of "tropic" and "solstice" is due to the observational fact that the Sun apparently "turns back" after reaching its northernmost (or southernmost) point in the sky where it seems to stand still (solstice, from L. solstitium, from sol "Sun" + -stit-, stes "standing", akin to stare "to stand", Greek histanai "to cause to stand", Sanskrit sthâ- "to stand", Avestan stâ- "to stand", Persian istâdan "to stand", Indo-European root: *stâ- "to stand").
The term "tropic" is first attested around 1350-1400 in English with the meaning "either of the two circles in the celestial sphere which describe the northernmost and southernmost points of the ecliptic". Extended 1527 to the corresponding parallels of latitude on the terrestrial globe, one (tropic of Cancer) 23°27' north, and the other (tropic of Capricorn) 23°27' south of the equator, being boundaries of the Torrid Zone. Meaning "region between these parallels" is from 1837. "Tropical" first used 1520-1530, and "tropical year" is first attested 1585-1595.
For an interesting account of the history of the tropical year, see Meeus & Savoie (1992).
10. For example, the Royal Greenwich Observatory/ National Maritime Museum website, states that: "The year is defined as being the interval between two successive passages of the Sun through the vernal equinox. Of course, what is really occurring is that the Earth is going around the Sun but it is easier to understand what is happening by considering the apparent motion of the Sun in the sky. The vernal equinox is the instant when the Sun is above the Earth's equator while going from the south to the north. It is the time which astronomers take as the definition of the beginning of Spring. The year as defined above is called the tropical year and it is the year length that defines the repetition of the seasons. The length of the tropical year is 365.24219 days". We notice the widely spread confusion between the tropical and vernal-equinox years, leading to an erroneous value given for the mean interval between two successive passages of the Sun through the vernal equinox. The correct value is 365.2424 days.
Other examples of the same mistake: "Tropical year: The year defined by two successive passages of the Sun through the vernal equinox: 365.242191 days" (Dictionary of Science and Technology, 1992, Academic Press, Inc.). "Tropical year: The time interval between two successive passages of the Sun through the vernal equinox. Its length is 365.2422 mean solar days." (Encyclopedia of Astronomy and Astrophysics, 2001, Institute of Physics Publishing).
11. The Gregorian calendar is also comparable to the vernal-equinox year in the sense that the prime and stated aim of the Gregorian reform was to keep the instant of the spring equinox from drifting away from the date of 21 March. Since the first Council of Nicaea in A.D. 325, 21 March had been adopted as the ecclesiastical date of the spring equinox for celebrating Easter: the first Sunday following the first ecclesiastical full moon that occurs on or after the day of the vernal equinox. The discussion of the accuracy with which the Gregorian calendar manages to keep the vernal equinox on 21 March is out of the scope of this note.
12. The Delta-T parameter, which can only be deduced from observations, depends strongly on the rotation rate of the Earth, which is uncertain at millisecond level. The Delta-T expression used in the present IMCCE ephemeris is:
Delta-T = 102.3 + 123.5 T + 32.5 T2 seconds
(Morrison & Stephenson 1982), where T is measured in centuries from the epoch J2000.0. Using a larger sample of observations of the historical solar and lunar eclipses, Stephenson & Houlden (1986) derive a more accurate expression for the Delta-T parameter pertaining to the epochs before A.D. 948:
Delta-T = 2715.6 + 573.36 T + 46.5 T2 seconds.
Moreover, according to a recent review by Stephenson (2002), the terrestrial spin rate is not continually decreasing, but undergoes variations with a cycle of about 1500 years whereby we are now in a centuries long period of no deceleration. Although the main causes of long-term changes in the length of the day are lunar and solar tides which produce a steady increase in the length of the day of approximately 2.3 milli-seconds per century, there is a significant non-tidal component causing a secular decrease in the length of the day at a mean rate of 0.6 milli-seconds per century. Therefore, a simple parabolic analysis of Delta-T is not an ideal representation of the reality. These variations, if confirmed by future research, should not have an important effect on the averaged IMCCE data presented in this paper. As for the current (epoch +2000) year length measured in real solar days (Table 4, column 1), the truth probably lies somewhere between the solar and uniform-day values.
13. Meeus (2002) has called the vernal-equinox year the equinox-equinox year. This also is misleading since the vernal and autumnal years are not identical.
14. The shape of the Earth's orbit around the Sun, described by a parameter called eccentricity, changes periodically due to the gravitational pull of the planets. The eccentricity varies between 0.070 (elongated ellipse) and 0.003 (almost circle) over some 100,000 years. Currently the eccentricity is 0.017, but will become nearly circular in about 25,000 years. As a result, the difference between the tropical and vernal-equinox years will tend to zero.
15. For more information about Mithra or Mehr, who has given his name to the 7th month of the Iranian calendar, and also its relation with Christmas and Marianne, the French symbol of the republic, see M. Heydari-Malayeri, The History of Marianne's Cap
http://wwwusr2.obspm.fr/~heydari/divers/marianne-engl.html
16. For a discussion of the name of the 4th Iranian month, see: M. Heydari-Malayeri, Tishtar, the Iranian Sirius (in preparation).
17. The fact that the 220-year cycle (with average year 365.2409 days) may be partitioned into 29- and 25-year cycles (220 = 5*29 + 3*25), would imply that Khâzeni had no use for the 33-year cycle (365.2424 days/year). Therefore, if no other information is available from Khâzeni, one would have to conclude that either he has been miscopied in the extant texts or that he misunderstood or disbelieved Khayyâm.
18. According to several historical indications, the Iranian calendar has been a source of inspiration for the creators of the French revolutionary calendar, who preferred a non-religious time reckoning system, based on natural seasons. As a matter of fact, during the age of enlightenment European scholars set out to know the Eastern cultures and civilizations in general. The first translation of the Zoroastrian sacred text Avesta in a European language was carried out by Abraham Anquetil-Duperron in French in 1771. It is also highly probable that the French revolutionary thinkers were aware of the Iranian calendar through several published works. We can, for example, mention: Freret, De 1'ancienne année des Perses, 1742, published in l'Histoire de l'Académie Royale des inscriptions et belles lettres, tome 16, Paris, 1751 and Gilbert, Nouvelles observations sur l'année des anciens Perses, in l'Histoire de l'Académie Royale des inscriptions, tome 31, Paris, 1788. For more information, see the recent interesting paper by Shafâ (2003) who highlights the Persian elements in the French revolutionary calendar.
References
- Abdollâhi, Rezâ, A.P. 1375 (A.D. 1996), Târix-e Târix dar Irân (The history of the calendar in Iran), Tehran, Amir Kabir (in Persian)
- Behruz, Zabih, A.P. 1331 (A.D. 1952), Taqvim va Târix dar Irân (Time reckoning & calendar in Iran), Tehran, Iran-kudeh, No 15 (in Persian)
- Birashk, Ahmad, 1993, A Comparative Calendar of Iranian, Muslim Lunar, and Christian Eras for 3000 Years, Mazda Publishers, Bibliotheca Persica, Costa Mesa, California and New York
- Biruni, Abu-Rayhân , c. 1000, Athar al-Baqia 'an al-Qurun al-Khalia, translated into English under the title The Chronology of Ancient Nations by Edward C. Sachau, London 1879 (William H. Allen)
- de Bloy, François, 1996, The Persian Calendar, J. Brit. Inst. Persian Studies 34, 39
- Borkowski, Kazimierz M., 1996/1997, The Persian calendar for 3000 years, Earth, Moon and Planets 74, No 3, 223
- Bretagnon, Pierre, Rocher, Patrick, 2001, Du Temps universel au Temps coordonnée barycentrique, Revue du Palais de la Découverte 285, février, p. 39
- Briant, Pierre, Histoire de l'Empire Perse, 1996, Fayard, p. 292
- Cassidy, Simon, 1996, Error in Statement of Tropical Year
- Encyclopedia Iranica, ed. Ehsan Yarshater, Columbia University, Eisenbrauns, Inc., Winona Lake, Indiana
- Malakpour, Iraj, 2004, private communication
- Meeus, Jean, 2002, More Mathematical Astronomy Morsels, William-Bell Inc., Richmond, Virginia, Ch. 63
- Meeus, Jean, Savoie, Denis, 1992, The history of the tropical year, J. Br. Astron. Assoc. 102, 1
- Morrison, L.V., Stephenson, F.R., 1982, Sun and Planetary System 96, 73, Reidel, Dordrecht
- O'Connor, John J., Robertson, Edmund F., 1999, The MacTutor History of Mathematics archive, Omar Khayyam
- Sayyâd, Mohammad R., 1981 (A.P. 1360), The sequence of quadriennial and quinquennial intercalations in the Jalâli calendar (in Persian), Proceedings of the 12-th Mathematics Conference, Isfahân University, p. 33
- Sayyâd, Mohammad R., 2000, Farhang, Quarterly J. of Humanities & Cultural Studies, vol. 12, No. 29-32, Issue topics: Commemoration of Khayyâm, p. 53 (in Persian)
- Seidelmann, P. K., Guinot, B., Doggett, L.E., 1992, in Explanatory Supplement to the Astronomical Almanac, University Science Books, Mill Valley, Californian, ed. P. K. Seidelmann, p. 80
- Shafâ, Shojâedin (2003), in Persian Heritage, No 30 (tâbestan-e A.P. 1382), p. 39 (in Persian)
- Simon, J.L., Bretagnon, P., Chapront, J., Chapront-Touzé, M., Francou, G., Laskar, J., 1994, Astron. & Astrophy. 282, 663
- Stephenson, F. Richard, 2003, Historical eclipses and Earth's rotation, Astronomy & Geophysics 44 (2), 2.22
- Stephenson, F.R., Houlden, M.A., 1986, Atlas of Historical Eclipse Maps, page x, Cambridge University Press
- Taqizâdeh, S. H., 1938, Old Iranian Calendars, Royal Asiatic Society
- Youschkevitch, A.P., Rosenfeld, B.A., 1973, "al-Khayyami", Dictionary of Scientific Biography VIII, p. 323
-
© Copyright 2004 by M. Heydari-Malayeri
![[calvin]](../images/home2.gif)
 Observatoire de Paris
Observatoire de Paris
 LERMA
LERMA
 Last updated 11 December 2006
Last updated 11 December 2006