Un nouveau regard sur le calendrier iranien

M. Heydari-Malayeri

Observatoire de Paris

Format PDF English version Persian version

1. Introduction

           Le calendrier iranien (ou persan) est solaire, et a la particularité de définir l'année par deux passages successifs et apparents du Soleil à l'équinoxe de printemps (vernal). Il est basé sur des observations astronomiques précises, et utilise en outre un système astucieux d'intercalations qui le rend plus précis que son homologue européen, le calendrier grégorien, pourtant plus récent. Il est actuellement utilisé en Iran en tant que calendrier officiel. Le calendrier iranien a un passé multi-millénaire, et trouve ses plus profondes racines dans la culture perse, et notamment dans l'héritage zoroastrien. Bien que cet article ne s'étende pas sur l'histoire du calendrier, car les questions auxquelles il tente de répondre ne le nécessitent pas, il présente un bref aperçu de ses origines les plus reculés. Le lecteur intéressé pourra trouver des informations détaillées à ce sujet dans, par exemple, Taqizâdeh (1938), Birashk (1993), Encyclopedia Iranica et Abdollâhi (1996). La version actuelle du calendrier provient d'une réforme conduite par le célèbre astronome, mathématicien et poète Omar Khayyâm (1048-1131 de l'ère chrétienne, désormais A.D.: Anno Domini), réalisée à l'équinoxe vernal de A.D. 1079 (le vendredi 21 mars; voir ci-dessous Note 1), ce qui correspond au premier Farvardin de l'A.P. (Anno Persico) 458. Le calendrier s'appelait aussi Jalâli, du nom du souverain qui a ordonné la réforme. A l'époque moderne, ses principes ont été officiellement adoptés par le parlement iranien le 31 mars 1925 (11 Farvardin A.P. 1304).

           La fête du Nouvel An, appelée Nowruz, du persan now "nouveau, neuf" + ruz "jour", est elle aussi un legs zoroastrien, aux multiples significations culturelles, et symbolise le réveil ou la renaissance de la nature après la stérilité de l’hiver (voir Note 2). Elle s’accompagne de cérémonies joyeuses, traditions vielles de plusieurs milliers d'années, qui ont lieu plusieurs jours ou semaines avant et après l'équinoxe de printemps. On peut citer, par exemple, le grand nettoyage de la maison qui précède Nowruz, la culture de graines en pots et la fête du feu qui a lieu la veille du dernier mercredi de l'année ainsi que le pique-nique de masse en campagne verdoyante le 13ème jour de la nouvelle année. Il y a d'autres festivités, mais leur explication sort du cadre de cet article. Nowruz a été célébré durant des millénaires par tous les peuples vivant en Asie occidentale et centrale (et parmi lesquels on compte Afghans, Azéris, Caucasiens, Kazakhs, Kurdes, Kirghiz, Tadjiks, et Turkmènes), et ce indépendamment de leur ethnicité, religion ou langue. Au delà de son message profond, le fait que Nowruz ne soit spécifique ni à une ethnie, ni à une religion en particulier, semble être l’une des principales raisons pour lesquelles Nowruz s’est érigé en héritage commun à tant de peuples divers.

           Le calendrier iranien, malgré sa remarquable stature, notamment sa précision et son caractère rationnel basés sur les observations astronomiques, reste mal connu en Occident. En réalité, peu d'études ont analysé les éléments fondamentaux de son système à la lumière des résultats astronomiques nouveaux, bien que plusieurs œuvres aient été consacrées à l'histoire des origines du calendrier. Il est, en particulier, nécessaire de souligner la durée réelle de l'année dans le calendrier iranien, car il y a actuellement une confusion généralisée entre le concept moderne de l'année "tropique" et celui d'équinoxe vernal sur lequel se base le calendrier iranien. Et cette confusion peut éventuellement perturber ou même endommager le calendrier. L'un des objectifs de cet article est donc de clarifier le concept de l'année dans le calendrier iranien.

           Cet article n'est pas uniquement destiné aux spécialistes du calendrier, mais se veut également à la portée des non experts. Après cette Introduction, la Section 2 présente une description générale du calendrier iranien. Ensuite, nous définissons l'année dans la Section 3, et discutons de sa durée à l'appui des résultats astronomiques obtenus tout récemment. Dans la Section 4 l'accent est mis sur la différence entre les années "tropique" et d'équinoxe vernal, tandis que le système d'intercalation, basé sur un cycle de 33 ans, sera décrit dans la Section 5. Bien que cet article s'intéresse essentiellement au fondement astronomique du calendrier, les aspects historiques n'ont pas été ignorés et la Section 6 présente, en particulier, une brève note sur l'un des aspects historiques de la réforme conduite par Khayyâm. Il n'y a guère longtemps, certains experts en calendrier iranien ont suggéré l'existence d'un cycle de 2820 ans dans le calendrier iranien. Nous discutons de cette question dans la Section 7 et soulignons les défauts d'un tel schéma. Nous abordons la correspondance entre le calendrier iranien et les autres systèmes dans la Section 8, et présentons quelques remarques sur l'origine ancienne du calendrier iranien dans la Section 9. Enfin, les conclusions apparaissent dans la Section 10. Tout au long de cet article, des explications complémentaires ont été fournies sous forme de 16 notes qui sont regroupées à la fin de l'article.

2. Description générale

           Nowruz commence à l'instant précis où le Soleil, dans son annuelle course apparente à travers le ciel, coïncide avec l'équinoxe vernal, événement qui peut se produire à n'importe quel moment de la période diurne de 24 h. Les équinoxes de printemps et d'automne sont définis comme points d'intersection entre l'écliptique (trajet apparent du Soleil) et l'équateur céleste (projection de l'équateur terrestre sur le ciel), bien que l'équinoxe de printemps (Note 3) soit le point de référence à partir duquel on mesure les ascensions droites (système équatorial) et les longitudes (système écliptique). L'équinoxe de printemps est également le moment où le Soleil semble traverser l'équateur céleste dans son voyage vers le Nord. Cependant il est de nos jours plus convenablement défini comme le moment où la longitude écliptique du Soleil atteint le degré zéro. L'événement de Nowruz est actuellement mesuré avec une précision meilleure que la milliseconde (Malakpour 2004). En utilisant les éphémérides calculées par l'Institut de Mécanique Céleste et de Calcul des Ephémérides (IMCCE) pour la période grégorienne A.D. 1583-2500, on trouve que 584 des équinoxes, soit environ 64% de la totalité des événements, ont lieu le 20 mars à la longitude de Téhéran. La répartition des événements pour les dates voisines est présentée dans la Table 1. Chaque année l'équinoxe de printemps arrive avec un retard, généralement inférieur à 6h, par rapport à l'événement précédent. Ce retard représente aussi la fraction du jour excédant les 365 jours entiers de l'année. Or la date de l'équinoxe vernal ne suit pas cette dérive systématique vers le futur car les retards accumulés sont compensés, dans le calendrier iranien, par le jour supplémentaire bissextile qu'on y rajoute tous les quatre ou cinq ans (voir ci-dessous, Section 5).

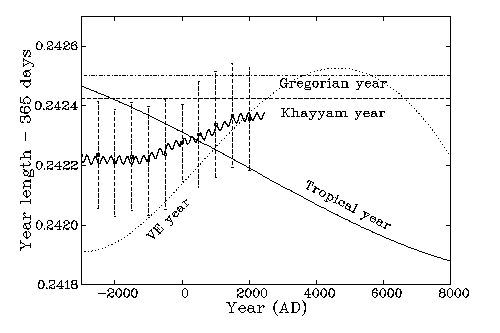
           Les données IMCCE nous ont également permis de calculer le retard ou le décalage dt = t(n+1) - t(n) pour l'intervalle A.D. +1000 à +2500, t étant l'instant de l'équinoxe vernal pour l'année n. On obtient une valeur moyenne de 5.81662 h ± 0.00240 (écart-type) ou 5h 48m 59.83s ± 8s (e.t.). Les bornes inférieure et supérieure, 5.54111 et 6.06444 h appartiennent respectivement aux années 1095 (A.P. 474) et 1216 (A.P. 595). Le diagramme représentant la variation du retard, dt, au cours des années est présenté dans la Figure 1. Le décalage moyen dépend de l'intervalle en question, du fait que la durée de l'année n'est pas constante (voir Section 3). La Table 2 montre le décalage pour divers intervalles ainsi que la durée moyenne de l'année, en temps solaire réel, correspondant à deux passages successifs du Soleil à l'équinoxe vernal.

Table 1. Dates de l'équinoxe vernal iranien pour la période A.D. 1583-2500

Date (mars)	Fréquence	Pourcentage
18	0	0
19	33	3.6
20	584	63.6
21	301	32.8
22	0	0

Figure 1. La variation du retard entre un événement de l'équinoxe vernal et l'événement suivant pour la période A.D. 1000-2500. Valeur moyenne: 5h 48m 59.8s. Cliquer sur l'image pour obtenir une meilleure résolution.

           Le premier jour de l'année ne peut évidemment pas commencer à l'instant même de l'équinoxe de printemps et le fait donc à minuit (le temps solaire réel de Téhéran), début du jour selon une très ancienne tradition iranienne (Note 4). Par conséquent, si l'équinoxe vernal a lieu avant midi, ce même jour est décrété premier jour de l'an. En revanche, si l'équinoxe a lieu après midi, l'année débutera le jour suivant. En d'autre termes, l'année commence au minuit le plus proche de l'équinoxe vernal. Dans le passé, on déterminait l'instant de l'équinoxe en observant l'altitude du Soleil à midi et on déclarait Nowruz le jour où l'altitude solaire dépassait celle de l'équateur céleste. Bien que l'année du calendrier puisse commencer avec un retard ou une avance allant jusqu'à 12h par rapport à l'événement de l'équinoxe, l'instant exact de l'équinoxe vernal (tahvil-e sâl) a une importance culturelle capitale. Quel que soit le moment, jour ou nuit, tous les membres de la famille, lavés et habillés de vêtements neufs, attendent le phénomène astronomique autour d'une table de cérémonie (haft-sin) sur laquelle sont disposés plusieurs objets symboliques. De nos jours, l'instant de Nowruz est annoncé par les stations de radio et de télévision, alors que jadis étaient utilisés coups de canons, grosses caisses et instruments à vent pour signaler l'événement. L’arrivée du moment précis déclenche explosions de joie et échanges de vœux.

Table 2. Retard moyen entre deux équinoxes vernaux successifs

Période	Décalage (heure) (h, m, s)	Année moyenne (jours solaires)
-4000 à +2500	5.81458 5h 48m 52.5s	365.242274
0 à +2500	5.81603 5h 48m 57.7s	365.242335
+1000 à +2500	5.81662 5h 48m 59.8s	365.242359
+1500 à +2500	5.81669 5h 49m 0.1s	365.242362
+1800 à +2200	5.81537 5h 48m 55.3s	365.242307
+800 à +1200	5.81609 5h 48m 57.9s	365.242337
+1995 à +2005	5.83087 5h 49m 51.1s	365.242953

           Le point de départ du calendrier iranien actuel est l'équinoxe vernal qui a eu lieu le vendredi 22 mars de l'année A.D. 622 (Note 5). Historiquement, le 22 septembre de cette année (7ème jour du mois arabe Rabi' I), le prophète de l'Islam émigra à Médina (Hijra). Or le second Calife Umar ibn al-Khatab, lors de la création du calendrier musulman, vers A.D. 638, préféra placer le début du calendrier islamique deux mois et huit jours avant le voyage du prophète, au début du Muharrams, le mois sacré des Arabes. Cette date correspond au 19 juillet A.D. 622. Par ailleurs, le fait que les mois du calendrier lunaire ne soient pas liés aux saisons et que les dates varient par rapport au cycle solaire rend ce calendrier inadapté à l'administration civile (par exemple pour la programmation de l'agriculture et pour la collecte des taxes). Par conséquent, les problèmes engendrés par le calendrier lunaire ont été fortement ressentis plusieurs siècles plus tard, en Iran, sous le règne de Jalâl ed-Din Malek Châh, de la dynastie des Saldjuqides; la célébration de Nowruz avait de plus dérivé au milieu du signe du Poisson, conséquence de l’abandon des intercalations (voir Section 5). En fait, selon les historiens et les astronomes contemporains de l'époque de la réforme, le principal objectif de cette entreprise a été de fixer Nowruz à l'équinoxe vernal (Encyclopedia Iranica).

           Pour les raisons que nous venons de mentionner, Nezâm-ol-Molk, grand vizir et éminente figure politique, persuada Malek Châh de réformer le calendrier. Il désigna un groupe d'astronomes dont il confia la direction à Omar Khayyâm (Note 6). Celui-ci mit sur pied un observatoire astronomique à Ispahan, capitale de l’époque (cependant, certaines sources ont mentionné les villes de Rey ou Neyshâpur). A la suite d’observations et de calculs, le comité de réforme adopta l'équinoxe vernal de A.D. 622, ce qui plaça le début du calendrier iranien six mois avant le Hijra. Par ailleurs, fut inventé un système unique d'intercalations, basé sur un cycle de 33 ans, décrit ci-dessous (Section 5). En outre, le comité adopta 12 mois égaux de 30 jours chacun, et inséra le reste de 5 ou 6 "jours volés" ou andargâh (épagomène) entre le 30 Spandarmad (Esfand) et Nowruz, comme cela se pratiquait dans le calendrier iranien pré-islamique. Et, chose fort intéressante, le comité rétablit les anciens noms persans des mois (Table 3), bien que d'autres alternatives aient été considérées et que de nouveaux noms persans aient été suggérés.

Table 3. Mois et saisons du calendrier iranien

Ordre	Avestique (A.D. c. -2000 à -300)	Persan moyen (A.D. c. -300 à +700)	Persan moderne	Jours	Saisons
1	Fravashi/Fravarti [l’essence divine]	Frawardîn	Farvardin	31	Printemps
2	Asha Vahishta [la plus grande des vertus]	Ardawahisht	Ordibehesht	31	Printemps
3	Haurvatât [l’intégrité]	Khordâd	Khordâd	31	Printemps
4	Tishtrya [Sirius, l’étoile de pluie]	Tîr	Tir	31	Eté
5	Amérétâ [(l’immortalité]	Amurdâd	Mordâd/Amordâd	31	Eté
6	Khshathra Vairya [la suprématie du choix]	Shahrewar	Shahrivar	31	Eté
7	Mithra [le Soleil, l’amitié, la promesse]	Mihr	Mehr	30	Automne
8	Ap [l'eau]	Âbân	Âbân	30	Automne
9	Âthra [le feu]	Âdur	Âzar	30	Automne
10	Dathushô [le créateur]	Day	Dey	30	Hiver
11	Vohu Manah [l’esprit de bien]	Wahman	Bahman	30	Hiver
12	Spéntâ Ârmaiti [la sainte sérénité]	Spandarmad	Esfand	29/30	Hiver

           On peut donc en déduire que le but de cette réforme n'a pas simplement été de résoudre les problèmes administratifs et économiques, mais également de conserver Nowruz, constituant essentiel de l'identité iranienne (au sens large du terme). La réforme a surtout eu une conséquence remarquable et probablement sans précédent dans l'histoire de l'Iran: elle attacha étroitement Nowruz à l'équinoxe vernal, ce qui semble n'avoir pas été le cas dans le calendrier zoroastrien sassanide. En effet, ce dernier n'utilisait apparemment pas les années bissextiles tous les quatre ans, mais rajoutait en revanche un mois supplémentaire au calendrier tous les 120 ans (de Blois 1996).

           Contrairement au calendrier islamique, qui est basé sur le mois lunaire synodique et l'année lunaire de 354 jours qui en découle, le calendrier iranien se divise en 12 mois qui sont liés aux vraies saisons solaires. Les 6 premiers mois du calendrier moderne ont 31 jours, les 5 mois suivants 30 jours et le dernier 29 ou 30 jours. Ce schéma de la durée des saisons est tout à fait conforme au fait que les saisons n'ont pas toutes la même longueur; le printemps et l'été étant plus longs que l'automne et l'hiver (Note 7). Le nom des mois, dans leur version avestique d'origine (Note 8), leurs significations et leur évolution linguistique au cours des âges sont présentés dans la Table 3.



3. Durée de l'année

           L'année iranienne est "tropique" et commence à l'équinoxe vernal. Néanmoins, on ne doit pas la confondre avec l'année tropique définie par les astronomes modernes (Note 9). A l'heure actuelle, l'année tropique se définit comme l'intervalle de temps pendant lequel la longitude moyenne du Soleil, par rapport à l'équinoxe moyen de la date, s’accroît de 360 degrés. Cette définition a été adoptée par l'Union Astronomique Internationale (IAU) lors de son Assemblée Générale, à Dublin, en 1955 (Seidelmann et al. 1992). Plusieurs chercheurs, notamment Meeus & Savoie (1992), Cassidy (1996) et Meeus (2002) ont souligné la différence entre l'année de l'équinoxe vernal et cette année tropique nouvellement introduite. Cependant l’amalgame entre les deux concepts est malheureusement largement répandu. En fait, la plupart des astronomes et des experts en calendrier définissent l'année tropique comme la période de temps correspondant à deux passages successifs du Soleil à l'équinoxe vernal, mais utilisent dans leurs calculs la durée de l'année issue de la nouvelle définition (Note 10). C'est une erreur, et, malheureusement, certains chercheurs iraniens ne manquent pas de la commettre.

           Il faudrait souligner que ce nouveau concept d'année tropique, établi pour les études mécaniques célestes, repose sur la longitude moyenne du Soleil et ne dépend pas d'une origine particulière pour le mouvement apparent annuel du Soleil. Il a pour but l'étude du comportement à très long terme de l'année en tenant compte de la précession (les termes séculaires) et non pas des perturbations gravitationnelles périodiques à court terme. Quelle que soit l'importance de ce concept, les calendriers solaires traditionnels, aussi bien iranien que grégorien (Note 11), sont basés sur la durée moyenne de l'année d'équinoxe vernal vraie. La situation actuelle de la nomenclature prête donc à confusion, car on utilise le même terme (année tropique) pour deux concepts différents mais très proches. Il serait par conséquent opportun que l'Union Astronomique Internationale procède à un éclaircissement de la situation, en adoptant deux termes distincts pour les deux notions. Il serait logique d'utiliser "l'année tropique" dans sa signification mécanique céleste moderne, et d'employer le terme "d'année d'équinoxe vernal" pour l'intervalle entre deux passages successifs du Soleil à ce point de référence. Tout naturellement, les Iraniens l'appellent l'année de Nowruz.

           Examinons maintenant la différence entre les années tropique et d’équinoxe vernal. Bretagnon et Rocher (2001) donnent l'expression suivante pour la durée de l'année tropique:

365.24219052 - 61.56 10^-6 T - 68.4 10^-9 T² + 263.0 10^-9 T³ + 3.2 10^-9 T⁴     [1]

T étant le temps dynamique barycentrique (TDB) ou, plus simplement, les jours uniformes (des éphémérides) de 86400 secondes (Temps Atomique International, TAI), comptés en milliers d'années juliennes (de 365250 jours) à partir de l'époque J2000.0. Cette expression a un domaine de validité de ±10,000 ans de part et d'autres de l'époque actuelle. Exprimé en temps universel, lié à la rotation de la Terre autour de son axe, les mêmes auteurs donnent la formule suivante pour l'année tropique:

365.2421789 - 135.63 10^-6 T - 68.4 10^-9 T² + 263.0 10^-9 T³ + 3.2 10^-9 T⁴    [2]

T représentant ici le temps universel. Nous constatons que la durée de l'année tropique à l'époque de J2000 a été de 365.24219052 jours uniformes de 86400 secondes, équivalent à 365.2421789 jours solaires réels, les deux pouvant être arrondis à 365.2422 jours. Les formules [1] et [2] indiquent également que la durée de l'année tropique n'est pas constante. Comme cela se lit aussi sur la Figure 2, sa durée, en jours uniformes, diminue d'environ 5 millisecondes par an car la précession s'accélère actuellement. De plus, sa durée, en jours solaires réels, décroît aussi d'environ 6 millisecondes supplémentaires par an en raison du ralentissement de la rotation terrestre, surtout sous l'effet de marée de la Lune. Il faudrait souligner aussi qu'à l'heure actuelle nous sommes incapables de prévoir d'une manière précise la durée du jour. En effet la rotation terrestre subit plusieurs variations irrégulières et imprévisibles sur diverses échelles de temps, les irrégularités étant engendrées aussi bien par les processus géophysiques internes et externes que par des perturbations astronomiques.

           Par ailleurs, l'intervalle moyen entre deux équinoxes vernal successifs, obtenu par Meeus (2002) pour la vraie longitude du Soleil en utilisant les éléments d'orbite de la Terre (Simon et al. 1994) et la solution exacte de l'équation de Kepler, est représenté par l'expression polynomiale suivante:

365.2423748 + 10.34 10^-5 T - 12.43 10^-6 T² - 22.63 10^-7 T³ + 1.31 10^-7 T⁴     [3]
celle-ci est valable pour la période allant de A.D -500 à +4500, où T est compté en milliers d'années juliennes de 365250 jours uniformes (des éphémérides) à partir de J2000.0. Il serait bon de mettre l’accent sur le fait que cette expression représente l'évolution globale de l'année d’équinoxe vernal réelle au cours de grands laps de temps en admettant le mouvement keplerien non-uniforme de la Terre. Cependant, elle ne tient pas compte des fluctuations de la durée de l'année engendrées par diverses perturbations gravitationnelles périodiques. La solution exacte de l'année s'obtient dans les éphémérides de l'IMCCE par une équation qui compte 96 termes. L'équation [3], exprimée en jours solaires, est représentée par:

365.2423632 + 2.93 10^-5 T - 12.43 10^-6 T² - 22.63 10^-7 T³ + 1.31 10^-7 T⁴    [4]
           La comparaison entre les équations [3] et [1] ou [4] et [2] éclaircit le fait que les durées moyennes des années tropique et d’équinoxe vernal ne sont pas identiques. Par exemple, pour l'époque de +2000, la durée moyenne de l'année tropique est de 365.2421789 jours, tandis que celle de l'année d’équinoxe vernal équivaut à 365.242362 jours: elle est donc plus longue de 15.82 secondes. Tout comme la durée de l'année tropique a été arrondie à 365.2422 jours, on peut, par approximation, prendre pour durée de l'année d’équinoxe vernal le chiffre de 365.2424 jours. L'équation [3] montre de plus que l'année d’équinoxe vernal varie également avec le temps (voir aussi Figure 2). Aux alentours de l'époque -3000, elle avait une valeur de 365.241872 jours uniformes, alors que vers le début de l'ère chrétienne elle avait atteint 365.242138 jours uniformes. Elle augmente encore maintenant et atteindra sa valeur maximale, 365.242525 jours uniformes, vers l'époque de +5000. Par conséquent, la différence entre l'année d'équinoxe vernal et l'année tropique ne se limite pas seulement à leurs durées: leurs variations au cours du temps également sont dissemblables. Contrairement à l'année d'équinoxe vernal, l'année tropique décroît continuellement, au moins jusqu'à l'époque de +8000.

           La Figure 2 montre également le comportement de l'année d'équinoxe vernal réelle, en jours solaires, obtenue par les calculs de l'IMCCE. Etant donné que la durée de l'année réelle varie considérablement sur des périodes relativement courtes, sa variation est montrée de deux façons différentes pour une meilleure visibilité. Les points se trouvant au milieu des barres verticales représentent les valeurs moyennées sur des intervalles de 500 ans, alors que les barres elles-mêmes indiquent les écart-types correspondants. La fluctuation la plus petite appartient à l'époque 0, où la durée de l'année varie d’environ 20s, alors que l'étendue des fluctuations est deux fois plus grande pour l'époque +2000. Quant à la courbe onduleuse, elle montre les données IMCCE après leur lissage en utilisant une méthode de filtrage qui élimine toutes les variations dont la période est inférieure à 100 ans. Nous constatons donc que les fluctuations principales de la durée de l'année d'équinoxe vernal proviennent des perturbations de périodes relativement courtes. Si l'on utilise un lissage plus fort, la forme générale de l'année réelle rapprochera de l'année moyenne. Notez bien que afin de convertir les jours uniformes en jours solaires, il faut utiliser un paramètre de correction appelé le dérivé de Delta-T, qui peut être représenté par la différence entre les équations [1] et [2]. Cette correction augmente, d'une manière générale, la durée des années qui se trouvent avant l'époque +2000 et les réduit après cette époque (Note 12).

Figure 2. La durée des années tropique et d'équinoxe vernal en fonction du temps est respectivement montrée par les courbes pleines et en pointillés, toutes deux en unité de jours uniformes (des éphémérides). L'année d'équinoxe vernal réelle, en jours solaires, autrement dit l'année iranienne, obtenue par l'IMCCE, est aussi montrée de deux manières: les points noirs au milieu des barres verticales représentent les valeurs moyennées sur des intervalles de 500 ans, les barres étant les écart-types correspondants. De même, la courbe sinueuse montre une version lissée des données de l'année réelle dans laquelle les fluctuations ayant une période inférieure à 100 ans ont été supprimées. Les droites horizontales indiquent la durée de l'année selon Khayyâm et le calendrier grégorien respectivement. Elles sont à comparer avec la durée de l'année d'équinoxe vernal exprimée en jours solaires et issues des calculs IMCCE. Cliquer sur l'image pour obtenir une meilleure résolution.

           Comme cela a été indiqué plus haut, la durée de l'année d'équinoxe vernal réelle peut s'écarter considérablement de la valeur moyenne sur de courtes périodes surtout sous l'effet de l'attraction gravitationnelle de la Lune et des planètes. Ces fluctuations de la durée de l'année sont également visibles dans la Figure 1. Pour la période A.D. 1000-2500, l'année la plus courte, de 365.230880 jours, est A.D. 1095 et la plus longue A.D. 1216, avec 365.252685 jours, ou 365j 6h 3m 52.0s. La durée moyenne dépend de l'intervalle considéré, comme l'indique la Table 2. Nous constatons donc que vers l'époque de Khayyâm la durée moyenne de l'année d'équinoxe vernal, considérée sur un intervalle de 400 ans, A.D. 800-1200, était de 365.242337 jours solaires, ce qui représente aussi la valeur moyenne pour la période 0 à +2500. En bref, nous adoptons comme durée moyenne de l'année la valeur de 365.242362 jours, correspondant à un intervalle de temps centré sur l'époque actuelle avec une extension de 500 ans de part et d'autre, à savoir de +1500 à +2500.

4. Différence entre les années "tropique" et iranienne

           Nous tentons de donner ici plus d'explications afin de mettre en évidence le fait que l'année iranienne d'équinoxe vernal n'est pas la même que l'année tropique des spécialistes de la mécanique céleste. Etant donné que l'orbite terrestre est une ellipse, la vitesse orbitale de la Terre n'est pas uniforme. Au périhélie de son orbite, la Terre se trouve au plus près du Soleil et se déplace donc plus rapidement qu'en moyenne, tandis que à l'aphélie, lorsqu'elle est au plus loin du Soleil, elle va plus lentement. De même, en raison de la précession, l'équinoxe vernal régresse le long de l'écliptique de 50.3 secondes d'arc par an par rapport aux étoiles, en même temps que le grand axe de l'orbite de la Terre tourne dans le sens direct de 11.6 secondes d'arc par an. Par conséquent, lorsque le Soleil traverse le point vernal, après avoir passé une année dans son trajet apparent le long de l'écliptique, la Terre n'a pas fait un tour complet. Elle a fait un circuit complet sur une orbite déformée (à cause de la rotation de l'orbite) moins un petit arc. La Terre ne parcourt pas ce petit arc toujours avec la même vitesse, car cela dépend de la position de la Terre par rapport à son périhélie. Il en résulte que selon le point de départ choisi pour "l'année", le trajet complet s'effectue en un temps variable. Cela signifie que la durée de l'année tropique "réelle" dépend du point de référence choisi sur l'écliptique.

           Une formule mathématique simple peut faciliter l'explication. On peut représenter la durée de l'année par Y = T - t, où T est le temps nécessaire pour que le Soleil effectue un tour complet par rapport au périhélie et t le temps gagné parce que le point de référence s'approche du Soleil. Ce temps gagné se représente par le rapport de la longueur de l'arc, S, à la vitesse apparente du Soleil: t = S/V. Or, du fait que la longueur de l'arc est constante, t ne dépend que de la vitesse. Par exemple, lors de solstice d'hiver en décembre, la Terre se trouve près du périhélie (auquel elle accède en début de janvier) et le Soleil se déplace vers le point de solstice apparemment plus vite qu'en moyenne. Par conséquent le temps gagné est plus petit que lorsqu'il s'approche de l'équinoxe vernal, et l'année tropique mesurée à partir de ce point non seulement sera plus longue que celle rapportée au point vernal, mais elle sera la plus longue parmi les quatre années cardinales. Meeus (2004) a obtenu la durée moyenne des diverses années tropiques, ou les intervalles entre deux passages successifs du Soleil aux points des saisons, à partir des éphémérides planétaires calculées par Simon et al. (1994). Les résultats, présentés dans la Table 4 (Note 13), manifestent que ces années n'ont pas la même longueur. Et nous voyons bien que l'année d'équinoxe vernal diffère de l'année tropique. En fait, l'année tropique représente la valeur moyenne parmi les quatre années de saisons (Note 14). Il faut souligner que les durées données dans la Table 4 sont en jours uniformes, et doivent être converties en jours solaires pour l'usage du calendrier, ce que nous avons fait pour l'année d'équinoxe vernal seulement (Note 12).

Table 4. Diverses années "tropiques" pour des époques variées *

Epoque	Année d'équinoxe vernal (Nowruz)	Année de solstice d'été	Année d'équinoxe d'automne	Année de solstice d'hiver
-1000	365.242022 365.24223	365.241859	365.242718	365.242871
0	365.242138 365.24227	365.241726	365.242496	365.242883
+1000	365.242261 365.24232	365.241648	365.242257	365.242840
+2000	365.242375 365.24236	365.241627	365.242018	365.242741
+3000	365.242464 365.24237	365.241659	365.241800	365.242594
+4000	365.242516 365.24235	365.241734	365.241620	365.242407

* Durée des années en unités de jours uniformes, sauf pour l'année d'équinoxe vernal qui est aussi donnée en jours solaires réels.

           La durée de l'année dans le calendrier iranien, telle que conçue par Khayyâm et al. est de 365.2424.. jours (Youschkevitch & Rosenfeld 1973), ce qui découle logiquement du système d'intercalation adopté: 365 + 8 / 33 = 365.2424.. (voir Section 5). Cette valeur est en bon accord avec la durée de l'année à l'époque de Khayyâm, 365.2423 jours, comme nous l'avons expliqué plus haut. L'estimation de Khayyâm s'accorde encore mieux avec la valeur de l'année actuellement: 365.2424 jours. En comparaison avec la durée de l'année grégorienne de 365 + 1 / 4 - 1 / 100 + 1 / 400 = 365 + 97 / 400 = 365.2425 jours, il est possible d'affirmer que la valeur de Khayyâm repose sur une connaissance plus rigoureuse du mouvement annuel du Soleil. Il est à noter qu'une estimation extrêmement précise de la durée de l'année (de 365.24219858156 jours) a été il y a peu attribuée à Khayyâm (O'Connor & Robertson 1999), bien qu'aucune source historique ne l'atteste, pour autant que nous le sachions. Nous pensons que ce chiffre ne provient pas de Khayyâm mais probablement du cycle erroné de 2820 ans qui a été proposé récemment (voir Section 7).

           La connaissance précise de la durée de l'année est une chose, l'utiliser en pratique pour construire un système de calendrier en est une autre, car l'année de calendrier de 365 jours entiers n'est pas égale à l'année solaire réelle. Le bon calendrier est donc celui dont le système d'intercalation rend une durée pour l'année la plus proche de la réalité.

5. Système d'intercalations

           Le décalage moyen de temps, dt, entre deux équinoxes vernaux successifs, présenté dans la Table 2, indique également la fraction de jour supplémentaire par rapport à une année de calendrier de 365 jours entiers. Autrement dit, chaque année, le temps solaire avance de dt/24 jour par rapport au temps du calendrier. Si l'on prend dt = 5.81662 h correspondant à l'intervalle +1000 à +2500, cette avance sera de 5.81662/24 = 0.242359, ou environ 0.2424 jour par an. Par conséquent, après quatre ans, l'avance équivaudra à 4 x 0.24236 = 0.96944 jour, s'approchant d'un jour entier, ce qui nécessite une année bissextile. Cette correction de 1 jour tous les 4 ans est néanmoins trop généreuse, et mène à une avance de l'année du calendrier sur l'année solaire. Ce point constitue le problème fondamental des calendriers solaires, et c'est pour cette raison que dans le calendrier iranien l'année bissextile n'est pas systématiquement appliquée tous les quatre ans (voir ci-dessous). D'autre part, si l'on n'appliquait pas les intercalations, la fête de Nowruz reculerait par rapport à l'équinoxe vernal pour faire un tour complet des saisons en 1506 ans. Plus précisément, après 4 ans, l'équinoxe aurait lieu le 2 Farvardin et après 8 ans le 3 Farvardin et ainsi de suite. En même temps, la fête de Nowruz dériverait de plus en plus vers l'hiver.

           Le calendrier iranien possède un système d'intercalations basé sur un cycle de 33 ans, qui consiste en 33 x 0.2424 = 7.9992 = 8 années bissextiles de 366 jours et 25 années ordinaires de 365 jours. Il y a deux types d'années bissextiles: i) l'année bissextile après 3 années ordinaires (appelée quadriennale), ii) l'année bissextile après 4 années ordinaires (quinquennale). Au cours d'une période quadriennale, l'équinoxe vernal a lieu par paire de deux, systématiquement deux fois après midi et ensuite deux fois avant midi. Or, tous les 33 ans environ, un équinoxe vernal survient très près de minuit entre les deux paires formant une période quinquennale. Plus explicitement, cette situation se produit surtout tous les 33 ans, et parfois, beaucoup moins fréquemment, après un intervalle de 29 ans.

           La première année du cycle de 33 ans est quinquennale et les sept autres quadriennales. On applique donc les intercalations aux années: 5, 9, 13, 17, 21, 25, 29, 33. Le cycle total s'élève à 25 x 365 + 8 x 366 = 12053 jours de calendrier. En comparaison, la durée de temps solaire sera de 33 x 365.242362 = 12052.99795 jours de l'époque actuelle. Cela signifie que le cycle de 33 ans avance de 0.00205 jour, ou grosso modo de 3 minutes, par rapport au temps solaire. Pour cette raison, un cycle strict de 33 ans a besoin d'un ajustement ultérieur. En supposant une durée constante pour l'année d'équinoxe vernal, après environ 500 cycles, ou à peu près 16000 ans, l'avance accumulée s'élève à 1 jour. Cependant, étant donné que la durée de l'année diminue après l'époque de +3000 pour atteindre une valeur d'environ 365.24182 jours durant l'époque +8000, une période plus courte est nécessaire pour que le calendrier avance d’un jour complet sur le temps solaire. Quoi qu'il en soit, lorsque l'erreur totale s'élève à la fraction 1/33 de jour, il faut remplacer le cycle de 33 ans par celui plus court de 29 ans afin que le calendrier marche de pair avec le temps solaire. Il faut cependant souligner qu'il est inutile de procéder à des extrapolations détaillées s'étalant sur de longues périodes car la durée de l'année n'est pas constante et, en outre, des perturbations inconnues pourraient s'ajouter et avoir un effet considérable.

           Dans le passé, alors que Newton n'avait pas encore proposé sa théorie de la gravitation et Laplace, Lagrange, Euler, Hamilton et les autres n'avaient pas contribué à la formulation de la mécanique céleste, on prévoyait l'instant précis de l'équinoxe vernal en extrapolant des observations détaillées. Aujourd'hui, grâce aux progrès remarquables dans les modèles des corps en orbite, et plus particulièrement l'avènement des ordinateurs puissants et des méthodes numériques, l'instant de l'équinoxe se prévoit avec une haute précision. Néanmoins, les observations sont indispensables pour vérifier la correspondance entre le modèle mathématique et la réalité. Les observations constituent aussi une partie importante de la culture iranienne du calendrier, et il serait avisé de conserver cette tradition. En outre, puisque l'astronomie amateur a fait des avancées techniques importantes, un nombre plus important de gens peuvent participer à l'observation du mouvement du Soleil aux alentours de Nowruz. Et du fait que Nowruz est accompagné par plusieurs cérémonies et festivités publiques, une observation populaire et généralisée du Soleil peut apporter un complément joyeux à notre époque. Cela constituera également une bonne occasion d’enseigner l'astronomie et la connaissance du calendrier au grand public. On peut recommander la même chose pour l'observation du mouvement solaire lors de la fête de Mehregân en début de Mehr, le 7ème mois du calendrier, consacrée à la célébration de l'équinoxe d'automne (Notes 15 & Note 16).

6. Note d'intérêt historique

           Les informations concernant la réforme du calendrier ne nous sont pas directement parvenues de Khayyâm lui-même, mais au travers de brefs récits menés par des astronomes d’époques plus tardives. En fait, 13 ans après l'instauration de la réforme, Khayyâm tomba en disgrâce suite à la mort de Malek Chah et au meurtre de Nezâm-ol-Molk's par les Assassins, un ordre politico-religieux commandité par Hasan Sabbâh. Après la mort du souverain, son épouse régna en tant que régente pendant deux ans, et Khayyâm hérita de toute l’hostilité qu'elle avait manifesté à l'égard de son protecteur, Nezâm-ol-Molk, avec qui elle s’était querellé à propos de la succession royale. De surcroît, les Musulmans fondamentalistes, qui honnissaient Khayyâm en raison de sa libre pensée, manifeste dans ses quatrains, prirent de l'importance à la cour. Il est aussi fort probable qu'ils n’aient pas apprécié les audacieuses initiatives de Khayyâm pour sauvegarder et promouvoir la culture perse. Ils coupèrent court au budget de l'observatoire et mirent fin à ses activités, parmi lesquelles la réforme du calendrier (Youschkevitch & Rosenfeld 1973).

           Toutefois, il est indubitable que Khayyâm et ses collaborateurs ont inventé le système d'intercalations basé sur les années quadriennales et quinquennales. L'astronome Khâzeni (Note 6), qui probablement fit partie du groupe de réforme et qui, plus tard, sous le règne de Sanjar, fils de Malek Chah, créa le zij (tables et observations astronomiques) Sanjari, utilise les intercalations quadriennales/quinquennales, qui résultaient très probablement des travaux du groupe dirigé par Khayyâm. Khâzeni calcule, pour une période de 220 ans dans le calendrier Jalâli, 53 intercalations, dont 8 quinquennales et 45 quadriennales (Note 17). Deux siècles plus tard, l'important astronome et mathématicien Nasireddin Tusi (A.D. 1201-1274), directeur de l'observatoire de Marâgha, qui créa le Zij-e Ilkhani, et est reconnu pour avoir fait la critique la plus exhaustive du modèle de Ptolémée et avoir présenté un nouveau modèle mathématique des mouvements planétaires, donne des informations brèves mais très importantes au sujet de la réforme du calendrier Jalâli. Dans son Zij-e Ilkhani il affirme explicitement qu'une intercalation est employée tous les 4 ans, faisant une année de 366 jours, et qu’après 7 ou 8 intercalations quadriennales, on applique une intercalation quinquennale sur la base de l'induction. On remarque ici une référence implicite au schéma des cycles de 29 et 33 ans. Pour plus de renseignements sur diverses tentatives d'intercalations en relation avec le plan quadriennal/quinquennal par les astronomes à travers les siècles, voir Sayyâd (1981) et l'intéressant et récent ouvrage de Abdollâhi (1996), qui traite de toute l'histoire du calendrier iranien.

7. Le cycle présumé de 2820 ans

           Tout récemment, certains experts en calendrier iraniens, notamment les regrettés Behruz (1952) et Birashk (1993), ont suggéré l'existence de cycles jusqu'ici inconnus dans le calendrier iranien. Ils divisent particulièrement le calendrier en cycles de 2820 ans, eux-mêmes répartis en 21 sous-cycles de 128 ans et 1 sous-cycle de 132 ans (2820 = 21 x 128 + 132). Les sous-cycles de128 et 132 ans sont eux aussi morcelés en périodes de 29, 33 et 37 ans (128 = 29 + 3 x 33; 132 = 29 + 2 x 33 + 37). En bref, le cycle consiste en 2137 années ordinaires et 683 années bissextiles.

           Ce plan comporte plusieurs défauts. Il prétend que le cycle de 2820 ans représente la période après laquelle les équinoxes vernaux se répètent au même instant du jour. Or, l'examen des résultats des éphémérides de l'IMCCE ne nous permet pas de soutenir cette thèse, qui a d'ailleurs été critiquée par des chercheurs en calendrier, parmi lesquels les astronomes iraniens Malakpour (2004) et Sayyâd (2000). De plus, le cycle de 2820 ans prend une avance de 0.5 jour par rapport au temps solaire. En utilisant la durée actuelle de l'année d'équinoxe vernal, le cycle s'élève à 2820 x 365.242362 = 1029983.461 jours, tandis que le calendrier aura 2137 x 365 + 683 x 366 = 1029983 jours. Afin que le cycle demeure synchronisé avec le temps solaire, l'année doit avoir une durée de 365.2421986 jours, ou d'environ 365.2422 jours. Or ce chiffre, qui résulte aussi de la fraction 683/2820, semble constituer la durée de l'année tropique moderne, prise pour celle de l'année d'équinoxe vernal. Par conséquent, le schéma se retrouve mis en difficulté à plusieurs reprises sur une période de 2025 ans, par exemple: 21 mars A.D. -1, 21 mars A.D. 1600 et 21 mars A.D. 2025.

           Tout porte à croire que le cycle de 2820 ans est à l'origine de l'estimation extrêmement précise de la durée de l'année (365.24219858156 jours) attribuée à Khayyâm (voir ci-dessus, Section 4). En fait, la fraction 683/2820 implique une année de 365.2421985815603 jours, qui ressemble étrangement à la durée attribuée, ce qui jette un doute sur son authenticité. Cette valeur fallacieuse provient éventuellement d'une interprétation erronée qui attribue le cycle de 2820 ans à Khayyâm lui-même. Or aucun document historique ne lie Khayyâm à ce cycle (Sayyâd 2000). La confusion est probablement due au fait que Behruz (1952) proposa son schéma d'intercalations sous forme des tables qu'il appela "tables Khayyâmi", laissant ainsi la porte ouverte à la confusion.

           La conception d'un tel cycle semble donc provenir d'une confusion entre les années tropique et d'équinoxe vernal, comme nous l’avons expliqué précédemment. De surcroît, ce système complexe ne rend pas le calendrier plus précis, car le plan actuellement suivi de 33 ans est très efficace, et ce en dépit de sa simplicité.

8. Correspondance avec d'autres calendriers

           Il existe plusieurs logiciels dignes de confiance qui servent à convertir les dates et les jours de la semaine du calendrier iranien en d'autres système et vice-versa. On peut mentionner le "Khayam Program":

http://payvand.com/calendar
installé par Hossein Bâgher-Zâdeh pour la correspondance entre les calendriers iranien et grégorien. Les années bissextiles dans les cycles de 33 ans sont celles qui, après être divisées par le chiffre 33, conservent un reste de 1, 5, 9, 13, 17, 22, 26 et 30. Par exemple, l'année A.P. 1375, qui a débuté le 20 mars 1996 possède un reste de 22 et elle est donc bissextile. Et ces règles sont implantées dans le logiciel "Khayam program". Dans un article récent, Borkowski (1996/1997) soutient que l'algorithme utilisé dans le logiciel précité est valable pour la période A.D. 1799 à 2256 (A.P. 1178 à 1634). Il présente aussi un code concis qui reconstruit le dessein des années bissextiles pour un intervalle de près de 3000 ans.

           Un autre outil intéressant est le logiciel Calendrica 2.0, conçu sur la base des algorithmes présentés dans Calendrical Calculations: The millennium Edition, par Edward M. Reingold & Nachum Dershowitz. La version en ligne du logiciel:

http://emr.cs.iit.edu/home/reingold/calendar-book/Calendrica.html
permet la conversion non seulement entre les systèmes iranien et grégorien, mais également entre plusieurs autres calendriers, et notamment les calendriers: arménien, chinois, français révolutionnaire (Note 18), hébreu, hindou, islamique, maya, ainsi que la version mathématique erronée du calendrier iranien basée sur le cycle d'intercalation de 2820 ans.

9. Remarques sur l'origine ancienne du calendrier iranien

           Les premiers états iraniens ont été fondés par les Mèdes (728-550 av. J.-C.) et les Achéménides (550-330 av. J.-C.). Nous avons un certain nombre d'informations sur les calendriers en usage à l'époque achéménide, mais les documents pré-achéménides de l'histoire de l'Iran sont extrêmement rares et ne nous apprennent rien sur le calendrier de cette époque.

           Plusieurs indices historiques et archéologiques suggèrent que le calendrier administratif à l'époque des Achéménides était luni-solaire, probablement emprunté aux Babyloniens. Or, il y avait en parallèle un calendrier solaire iranien largement répandu parmi la population. La raison de l'adoption du calendrier babylonien était sûrement d'ordre politique. Les Achéménides (Cyrus le Grand lui-même?) voulaient sans doute utiliser le système administratif des Babyloniens, qui avaient plus d'expérience que les Perses. L'adoption de ce calendrier était également un signe de respect envers l'un des peuples qui constituaient l'empire achéménide, tout comme Cyrus le Grand rend hommage à Marduk, dieu suprême des Babyloniens, lors de la cérémonie de son couronnement. Abdollâhi (1996) avance plusieurs arguments convaincants en faveur de l'influence babylonienne, alors qu'il réfute fermement l'opinion émise par plusieurs chercheurs, selon laquelle le calendrier étatique achéménide était calqué sur le modèle égyptien.

           Briant (1996), un spécialiste des Achéménides, en se basant sur les auteurs antiques (Plutarque, Diodore, Quinte-Curce, Dicéarque) croit à l'existence d'un calendrier solaire de 360 jours et 5 jours épagomènes, qui existait concurremment avec le calendrier étatique officiel de type lunaire babylonien. On peut également mentionner un autre fait historique en faveur de l'existence d'un calendrier solaire ancien à l'époque achéménide. Nous savons avec certitude que le calendrier solaire zoroastrien a été adopté par les Cappadociens après la conquête de l'Asie Mineur par Cyrus le Grand, qui est entré dans Sardes en 547 av. J.-C. Ce calendrier solaire, qui consistait en 12 mois de 30 jours plus 5 jours épagomènes, était une réplique du calendrier zoroastrien compte tenu du nom et de l'ordre de ses mois (Encyclopedia Iranica). Rappelons qu'après la conquête de l'Asie Mineure, des Iraniens s'y sont installés et ont, entre autres, érigé des temples zoroastriens. Soulignons aussi que même au 4ème siècle de notre ère, 700 ans après la conquête d'Alexandre, beaucoup de villages en Cappadoce étaient peuplés d'Iraniens descendants des premiers colons. Or, le fait qu'à l'époque de la domination des Achéménides en Asie Mineure les Cappadociens ont emprunté le calendrier zoroastrien, et non pas le calendrier officiel d'état, souligne le profond enracinement de celui-ci parmi les Iraniens, surtout en ce qui concerne les affaires culturelles et religieuses de tous les jours. Cet enracinement suppose que le calendrier solaire zoroastrien soit beaucoup plus ancien que celui adopté par l'administration achéménide.

           Les documents historiques à propos du calendrier iranien à des temps très anciens sont tellement rares qu'aucune information n'est à négliger, surtout celles venant de Biruni (de Bloy 1996). En effet, de multiples informations données par Biruni sur le calendrier pré-islamique iraniens se sont avérées exactes (Abdollâhi 1996). Biruni, dans son Athar al-Baqia, nous renseigne sur le calendrier des Pishdâdis, période la plus ancienne de l'histoire traditionnelle de l'Iran qui commence par Kiumars, le roi mythologique. Les Pishdâdis sont suivis par les Kiyânis dont le dernier roi Dârâ (Darius III) est tué lors de la conquête d'Alexandre. Du fait que Biruni compte aussi Kourosh (Cyrus) et Ardashir (Artaxerxes I Longimanus) parmi les Kiyânis et identifie les Kiânis avec les Achéménides, les Pishdâdis sont plus anciens que les Achéménides. Et d'après les légendes, Nowruz a été établi par le roi Pishdâdi Jamshid (Yima/Yama de la tradition indo-iranienne) dont le temps remonte au début de la sédentarisation des peuples indo-iraniens et coïncide aussi avec une glaciation. Quoi qu'il en soit, ces légendes soulignent le caractère très ancien de Nowruz ainsi que son importance culurelle.

           Selon Biruni, les Pishdadis comptaient 360 jours dans une année et 30 jours dans un mois. Ils observaient donc un mois bissextile tous les 6 ans et appelaient l'année en question année bissextile. Puis, tous les 120 ans, ils avaient 2 mois bissextiles, l'un pour les 5 jours non-comptés, et l'autre pour les quarts de jour ignorés. On peut donc calculer la durée de l'année dans ce calendrier ainsi (Abdollâhi 1996):

un an = 12 x 30 = 360 jours
6 ans = 6 x 360 + 30 = 2190 jours
120 ans = 20 x 2190 + 30 = 43830 jours
43830/120 = 365.25 jours,

à savoir 365 jours et un quart de jour. Evidemment, ceci n'est vrai que dans un calendrier solaire. Par conséquent, si on en croit Biruni, les Iraniens d'avant les Achéménides utilisaient un calendrier solaire. Et selon les spécifications décrites ci-dessus, il devait s'agir du calendrier zoroastrien. On peut en déduire que, contrairement à une idée reçue, les Egyptiens n'étaients pas les seuls parmi les civilisations anciennes d'avoir un calendrier solaire. Nous ne savons pas exactement quand celui-ci a commencé. Or, selon Biruni, c'est Zoroastre lui-même qui a fondé le système du mois bissextile. Bien que l'époque de Zoroastre ne soit pas clairement connue (certaines sources grecques l'ont placée à 6000 av. J.-C. alors que la tradition le situe à 600 av. J.-C.), l'étude récente des particularités linguistiques de Gathas (la partie la plus ancienne de l'Avesta attribuée à Zoroastre lui-même) suggèrent que Zoroastre vivait aux alentours de 1500 av. J.-C.

           A une certaine époque, le calendrier iranien a connu une réforme: au lieu d'observer un mois intercalaire tous les 6 ans, les 5 jours manquants, appelés andargâh, ont été insérés après le 360ème jour. La date du passage au calendrier de 365 jours est un sujet de débats. W.E. West a proposé 505 av. J.C., Markwart l'a estimé à 493-90, Boyce a dans un premier temps suggéré l'époque sassanide, mais a récemment révisé son estimation initiale et propose la période achaéménide (Encyclopedia Iranica): la question reste ouverte.

           L'élément le plus caractéristique du calendrier iranien est Nowruz, qui, dans les croyances zoroastriennes s'associe avec le feu, la septième création d'Ahura Mazda. Nowruz est en fait le festival le plus important dans le calendrier solaire zoroastrien. Selon Boyce (op. cit. sous gâhanbârs), parmi les sept fêtes zoroastriennes très anciennes ``c'est seulement Nowruz qui semble avoir une justification doctrinale réelle, car le ``jour nouveau'' se célébrait à l'équinoxe de printemps, lorsque le Soleil, la représentation la plus puissante de la création du feu, prodigue au monde la chaleur et la vie renouvelées. ... Il semble hautement probable que Nowruz, avec sa signification théologique symbolique, soit établi par Zoroastre lui-même.''

10. En guise de conclusion

           Nous avons, dans cet article, présenté une description détaillée du calendrier iranien en mettant l'accent sur les phénomènes astronomiques qui le soutiennent, sans en ignorer les aspects historiques. Une caractéristique marquante de l'année iranienne est son point de départ, la fête de Nowruz, qui coïncide avec un événement astronomique: l'arrivée du Soleil au point de l'équinoxe vernal. Nowruz, qui symbolise la renaissance de la nature et le triomphe de la vie sur le froid et l'obscurité de l'hiver, est célébrée par un grand nombre de peuples en Asie occidentale et centrale.

           A partir des éphémérides de l'institut français IMCCE, relatives à la période A.D. -4000 à +2500, et des équations obtenues par Bretagnon & Rocher (2001) et Meeus (2002), nous avons discuté de diverses définitions de l'année et nous avons montré que le calendrier iranien se base sur l'année d'équinoxe vernal et non pas sur l'année "tropique".

           En réalité, le concept moderne d'année "tropique", formulé par les spécialistes de la mécanique céleste, représente une année moyenne qui ne dépend pas d'un point de référence sur l'écliptique. Elle ignore également les fluctuations à court terme dans la durée de l'année.

           Par conséquent, l'année "tropique", de 365.2422 jours, ne correspond pas du tout à l'intervalle (ni moyen ni vrai) entre deux passages successifs du Soleil à l'équinoxe de printemps. Attribuer la valeur de 365.2422 jours à un tel intervalle est une erreur, malheureusement largement répandue.

           En revanche, l'année iranienne, ou année d'équinoxe vernal vraie, dépend du mouvement non-uniforme keplerien de la Terre autour du Soleil ainsi que des perturbations à court terme. Il est donc nécessaire d'observer les passages successifs du Soleil à l'équinoxe vernal afin de déterminer l'instant de Nowruz et la durée réelle de l'année précédente.

           Si l'on ignore les fluctuations à court terme, la durée moyenne de l'année iranienne est à l'époque actuelle de 365.2424 jours solaires. Cela représente l'intervalle moyen entre deux passages successifs du Soleil à l'équinoxe de printemps.

           La différence entre les deux années "tropique" et d'équinoxe vernal ne se limite cependant pas à leur durée, car leurs variations à long terme sont également dissemblables.

           A part le fait que la confusion entre ces deux concepts de l'année est scientifiquement fausse, elle peut également entraîner d'autres erreurs et même miner la précision du calendrier iranien. Or, étant donné que l'importance de cette question échappe même aux astronomes et aux experts en calendrier, nous avons proposé d'utiliser deux termes distincts pour ces deux concepts, afin d'éviter la confusion: l'année "tropique" pour le concept nouvellement introduit et l'année d'équinoxe vernal lorsqu'il s'agit des calendriers solaires, iranien ou grégorien.

           La durée de l'année imposée par la réforme de Khayyâm est de 365.2424.. jours. Cette valeur est en bon accord avec la durée de l'année d'équinoxe vernal à son époque, qui était de 365.2423 jours en moyenne, et s'accorde encore mieux avec la durée actuelle de l'année, qui est en moyenne de 365.2424 jours.

           Nous avons analysé le système d'intercalation du calendrier iranien, qui repose sur un cycle de 33 ans, et avons expliqué les bases astronomiques de ce cycle, qui n'a pas d'égal dans d'autres calendriers. Il y a deux sortes d'années bissextiles dans ce calendrier, quinquennale et quadriennale. Le cycle de 33 ans contient 8 années bissextiles, la première étant quinquennale et les sept autres quadriennales.

           Enfin, nous avons expliqué les raisons pour lesquelles le cycle récemment proposé de 2820 ans est fallacieux, et avons argué qu'il provient probablement d'une confusion entre les années d'équinoxe vernal et "tropique". Non seulement ce cycle est erroné, mais un tel schéma d'intercalations semble également inutile pour le calendrier iranien, car le système actuel, basé sur le cycle de 33 ans, est presque parfait. Nous avons aussi avancé que ce schéma est à l'origine de la valeur extrêmement précise de la durée de l'année solaire récemment attribuée à Khayyâm.

Remerciements. C'est un grand plaisir de remercier l'Institut de Mécanique Céleste et de Calcul des Ephémérides (IMCCE) à Paris, Directeur Dr. William Thuillot, ainsi que Dr. Patrick Rocher qui ont mis à ma disposition les éphémérides qui ont été essentielles pour cette étude. De même, nos discussions m'ont été très profitables. Mon domaine de recherche en astrophysique étant bien en dehors de celui des calendriers et de la connaissance des temps, j'ai beaucoup appris au cours de la préparation de cet article et j'aimerais remercier tous ceux qui ont participé à ce projet. Je suis particulièrement redevable à Mr. Simon Cassidy, Emeryville Ca. U.S.A, expert en calendriers, pour de nombreux échanges e-mail et pour ses remarques critiques qui ont certainement contribué à améliorer le contenu de l'article. Je le remercie sincèrement. J'ai également bénéficié des discussions avec plusieurs de mes collègues de l'Observatoire de Paris: en particulier Dr. Thibaut Le Bertre, Dr. Jean-François Lestrade et Dr. James Lequeux. Qu'ils en soient remerciés. J'aimerais aussi remercier Dr. Vassilis Charmandaris, Université de Cornell, USA, pour ses commentaires. Ma reconnaissance va également à Mr. Frédéric Meynadier, Observatoire de Paris/Université Paris VI, pour sa coopération précieuse et efficace. Je voudrais remercier vivement Mr. Jean Meeus, Bruxelles, et Dr. Iraj Malakpour, Institut Géophysique, Téhéran, pour avoir répondu à mes questions. J'aimerais également exprimé ma gratitude à Drs. Edward M. Reingold & Nachum Dershowitz ainsi qu'à Dr. Hossein Bâgher-Zâdeh pour avoir utilisé leurs logiciels de conversion de calendriers. De même mes remerciement s'adressent à Dr. Kazimierz M. Borkowski, Observatoire de Radio Astronomie de Torun, Université Nicolaus Copernicus, Pologne, qui a lu le manuscrit et a fait plusieurs remarques intéressantes. Je remercie également Dr. Jafar Âghâyâni-Châvoshi, Université Sharif, Téhéran, de m'avoir procuré un certain nombre de documents historiques. J'adresse également mes sincères remerciements à Dr. M.-Sch. Adib-Soltâni, Téhéran, pour ses remarques, notamment d'ordre étymologique. Enfin, je tiens à dédier cet article à la mémoire des regrettés Zabih Behruz et Ahmad Birashk, qui ont initié les travaux de la recherche moderne sur le calendrier iranien.

Notes

1. Selon le calendrier grégorien. La date correspond au 15 mars dans le calendrier julien.

2. Etymologie de Nowruz. Le persan moderne now "nouveau", du persan moyen nôk, de l'avestique nava-, apparentés au sanskrit nava-, au grec neos, au latin novus, tous provenant de la racine indo-européenne *newos. Les mots anglais new, novel, allemand neu et français nouveau, neuf aussi appartiennent à ce groupe. La seconde composante, le persan moderne ruz "jour", du persan moyen rôc, du vieux perse raucah-, de l'avestique raocah- "lumière, brillant; lumière du jour", de la même racine que le sanskrit roka- "brillance, lumière", le grec leukos "blanc, claire", le latin lux "lumière" (aussi lumen, luna), l'indo-européenne *leuk- "lumière, brillance". Les mots persans rowshan "brillant, clair", foruq "lumière, lueur" et afruxtan "allumer" aussi appartiennent à cette famille, comme l'anglais light, l'allemand Licht et le français lumière.

3. Il n'y pas d'ambiguïté entre les équinoxes de printemps et d'automne, même si le passage du Soleil à l'équinoxe d'automne débute le printemps dans l'hémisphère austral! L'équinoxe vernal est le point ayant les coordonnées 0,0 degré dans le système écliptique, tandis que l'équinoxe d'automne est défini par le point 180, 0 degrés.

4. Selon plusieurs sources, placer le début du jour à minuit est une pratique iranienne ancienne. Par exemple, le savant renommé Abu-Rayhân Biruni (A.D. 973-1048) aborde ce sujet dans son célèbre Athar al-Baqia (histoire et géographie anciennes), écrit aux alentours de A.D. 1000 (voir ci-dessous, les références, pour plus de détails). Il souligne en outre que le zij de Shahriyâr, les calculs et les tables astronomiques établis sous le règne de l'empereur Sassanide Khosrow I Anushiravân vers A.D. 555, étaient basés sur l'adoption de minuit pour le commencement du jour. Notez bien que le choix de minuit pour le début du jour par les astronomes occidentaux est relativement récent. De fait jusqu'en 1925 les astronomes commençaient et terminaient leur jour à midi. Ainsi, initialement, le Temps Moyen de Greenwich (GMT) commençait et se terminait à midi moyen de Greenwich, alors que le Temps Civil de Greenwich (GCT) commençait à minuit. Ceci étant, les jours juliens utilisés par les astronomes commencent toujours à midi Temps Universel.

5. Il s'agit du calendrier grégorien. Cela correspond au 19 mars dans le calendrier julien. Taqizâdeh donne le 17 mars A.D. 622, or cette date est erronée, comme l'a fait remarquer Birashk le premier.

6. Selon plusieurs sources, jusqu'à huit astronomes ont participé au projet de réforme du calendrier. A part Omar Khayyâm, les autres noms mentionnés sont: Abu-Hâtam Mozaffar Esfazâri, Abd-ol-Rahmân Khâzeni, Meymun ebn-e Najib Vâseti et Abol-Abbas Lukari. Certains historiens ont semé le doute sur la participation de Khâzeni, un jeune esclave byzantin, à qui le maître Ali ebn-e Khâzen Marwazi, trésorier et chancelier de la cours à Marv (actuellement Mary en Turkmenistan), procura la meilleure éducation possible, de sorte qu'il devint un mathématicien, un astronome et un "physicien" réputé. Khâzeni établit un zij pour le souverain Sanjar, et inventa une balance (pour mesurer les gravités spécifiques) dont la précision fut inégalée jusqu'à la fin du 18ème début du 19ème siècle. Il décéda en A.D. 1115 ou 1130, ce qui n'est pas incompatible avec sa participation à la réforme du calendrier. Ceci étant, le système d'intercalations que Khâzeni propose dans son zij n'est pas tout à fait en accord avec le schéma de Khayyâm (voir aussi Note 17), et cela peut être interprété comme un signe de sa non-adhésion à la réforme du calendrier.

7. La durée actuelle des saisons astronomiques, autour de l'année 2000, est d'environ: 92.76 jours pour le printemps, 93.65 jours pour l'été, 89.84 jours pour l'automne et 88.99 jours pour l'hiver. Les saisons ne sont pas égales car l'orbite terrestre est légèrement elliptique et le Soleil ne se trouve pas exactement au centre de l'orbite. Selon la 2ème loi de Kepler, la Terre se déplace plus rapidement lorsqu'elle est plus près du Soleil. Par conséquent, les saisons qui correspondent à la période de l'année où la Terre se trouve plus près du Soleil s'écoulent plus rapidement. La Terre atteint le périhélie, son point orbital le plus près du Soleil, au début de janvier et se retrouve à l'aphélie, le point le plus lointain du Soleil, au début de juillet. Pour cette raison, l'été dure plus longtemps que l'hiver dans l'hémisphère nord. Dans l'hémisphère sud, c'est l'hiver qui est le plus long.

La situation actuelle n'est cependant pas éternelle et la durée des saisons varie au cours du temps en raison du changement des paramètres orbitaux de la Terre. La précession, ou mouvement de l'orientation de l'axe de rotation de la Terre, change la position des points du solstice et de l'équinoxe par rapport au périhélie. Ces points mettent environ 21,000 ans (précession climatique) pour faire un tour complet de l'orbite par rapport au périhélie. De même, la variation de la forme de l'orbite de la Terre, ou de l'excentricité (Note 12), qui a une période d'environ 100,000 ans, modifie la durée des saisons. Enfin, la variation de l'obliquité, ou l'inclinaison de l'axe de la Terre, produit des changements importants dans la quantité d'énergie solaire reçues sur Terre aux hautes latitudes, entraînant des altérations climatiques considérables. L'obliquité est actuellement de 23.5 degrés environ, mais elle varie entre 22.5 et 24.5 degrés, sur une période de 41,000 ans.

8. L'avestique, la langue de l'Avesta, les textes sacrés du zoroastrianisme, appartient au groupe iranien de la famille indo-européenne des langues. Il est actuellement admis en général que la partie la plus ancienne de l'Avesta, qui s'appelle Gathas (hymnes, chants) et se constitue des poèmes attribué à Zarathushtra lui-même, date des alentours du deuxième millénaire avant J.C., ce qui la rend contemporaine des Védas en Sanskrit.

9. "Tropique" du latin tardif tropicus "qui appartient, se rapporte au solstice", du latin tropicus "qui se rapporte à un tour", du grec tropikos "qui se rapporte à un tour ou un changement, ou au solstice" (comme nom, "le solstice"), de tropos "tour, changement, manière, style", tropein "tourner". La racine indo-européenne *trep- "tourner". D'autres termes de la même racine: troubadour, trouver, trophée, entropie.

La relation entre les notions de "tropique" et "solstice" provient du fait observationnel selon lequel le Soleil fait apparemment " demi tour " après avoir atteint son point le plus au nord (ou le plus au sud) dans le ciel, où il semble rester immobile ("solstice", du latin solstitium, de sol "Soleil" + -stit-, stes "debout", apparenté à stare "rester, s'arrêter; être debout", grec histanai "faire arrêter", sanskrit sthâ- "rester; être debout", avestique stâ- "rester, s'arrêter; être debout", persan istâdan "être debout; s'arrêter", racine indo-européenne: *stâ- "rester, etre debout").

Le terme "tropique" est attesté pour la première fois en français en 1377, et définissait "chacun des deux parallèles de la sphère céleste, de déclinaison + et – 23°27', qui passent par les points solsticiaux (points de l'écliptique qui sont à la plus grande distance du plan de l'équateur)". Son utilisation s'est étendue en 1532 pour désigner "chacun des deux parallèles de la sphère terrestre, de latitude + et – 23°27', qui limitent les régions dans lesquelles le Soleil passe deux fois par an au zénith: tropique du Cancer dans l'hémisphère nord, et tropique du Capricorne dans l'hémisphère sud". Le sens de "région entre ces deux parallèles, les tropiques, la zone tropicale" remonte à 1765.

Pour un récit intéressant de l'histoire de l'année tropique, voir Meeus & Savoie (1992).

10. Par exemple, le site web du National Maritime Museum website (une branche de l'ex-Royal Greenwich Observatory), affirme que: "The year is defined as being the interval between two successive passages of the Sun through the vernal equinox. Of course, what is really occurring is that the Earth is going around the Sun but it is easier to understand what is happening by considering the apparent motion of the Sun in the sky. The vernal equinox is the instant when the Sun is above the Earth's equator while going from the south to the north. It is the time which astronomers take as the definition of the beginning of Spring. The year as defined above is called the tropical year and it is the year length that defines the repetition of the seasons. The length of the tropical year is 365.24219 days". Nous constatons la confusion entre les années tropique et d'équinoxe vernal, produisant la valeur erronée donnée pour l'intervalle entre deux passages successifs du Soleil à l'équinoxe vernal. La valeur correcte est 365.2424 jours, comme cela a été expliqué dans le texte.

Autres exemples de la même erreur: "Tropical year: The year defined by two successive passages of the Sun through the vernal equinox: 365.242191 days" (Dictionary of Science and Technology, 1992, Academic Press, Inc.). "Tropical year: The time interval between two successive passages of the Sun through the vernal equinox. Its length is 365.2422 mean solar days." (Encyclopedia of Astronomy and Astrophysics, 2001, Institute of Physics Publishing).

11. Le calendrier grégorien aussi est comparable à l'année d'équinoxe vernal en ce sens que l'objectif principal et déclaré de la réforme grégorienne a été de garder l'instant de l'équinoxe vernal le plus près de la date du 21 mars. Depuis le premier concile de Nicée en A.D. 325, le 21 mars avait été adopté comme date ecclésiastique de l'équinoxe vernal pour la célébration de la fête de Pâques: le premier dimanche suivant la première pleine lune ecclésiastique qui a lieu le jour de l'équinoxe vernal ou après l'équinoxe vernal. Discuter de la précision avec laquelle le calendrier grégorien parvient à garder l'équinoxe de printemps au 21 mars est en dehors du sujet de cette note.

12. Le paramètre Delta-T s'obtient uniquement par des observations et dépend sensiblement de la vitesse de rotation de la Terre, qui est incertaine à l'échelle de la milliseconde. Le paramètre Delta-T utilisé dans les éphémérides de l'IMCCE s'exprime par la relation:

Delta-T = 102.3 + 123.5 T + 32.5 T²    secondes
(Morrison & Stephenson 1982), où T est compté en siècles à partir de l'époque J2000.0. Or Stephenson & Houlden (1986) obtiennent une formule plus précise pour les époques précédant A.D. 948 en utilisant un échantillon plus grand d'éclipses solaires et lunaires rapportées dans des documents historiques:

Delta-T = 2715.6 + 573.36 T + 46.5 T²    secondes.
En outre, selon une revue récente par Stephenson (2002), la vitesse de rotation terrestre ne diminue pas continuellement, mais subit des variations avec un cycle d'environ 1500 ans, dans lequel nous sommes actuellement en une période de non décélération qui dure plusieurs siècles. Bien que les marées lunaires et solaires soient les principales causes des changements à long terme dans la durée du jour, produisant une augmentation continue d'environ 2.3 millisecondes par siècle, il y a une composante indépendante des marées qui produit une diminution séculaire de la durée du jour de 0.6 milliseconde par siècle. Par conséquent, une analyse parabolique simple du paramètre Delta-T n'est pas représentative de la réalité. Ces variations, si elles sont confirmées par les recherches futures, ne doivent pas avoir un effet important sur les données moyennées de l'IMCCE présentées dans cet article. Quant à la durée de l'année à l'époque actuelle (+2000), mesurée en jours solaires réels (Table 4, colonne 1), la réalité doit se trouver entre les deux valeurs en jours solaires et en jours uniformes.

13. Meeus (2002) appelle l'année d'équinoxe vernal l'année d'équinoxe-équinoxe. Or ceci également est ambigu, car les années d'équinoxe vernal et d'équinoxe d'automne n'ont pas la même durée.

14. La forme de l'orbite terrestre autour du Soleil, décrite par un paramètre qui s'appelle excentricité, change périodiquement en raison de l'attraction gravitationnelle des planètes. L'excentricité varie entre 0.070 (ellipse allongée) et 0.003 (quasi circulaire) tous les 100,000 ans environ. L'excentricité a actuellement une valeur de 0.017, mais l'orbite deviendra presque circulaire dans quelques 25,000 ans. Par conséquent, la différence entre les années tropique et d'équinoxe vernal tendra vers zéro.

15. Pour plus d'informations au sujet de Mithra ou Mehr, qui a donné son nom au 7ème mois du calendrier iranien, ainsi que pour son lien avec la fête de Noël et Marianne, le symbole de la république française, voir M. Heydari-Malayeri, D'où vient le bonnet de Marianne? http://wwwusr2.obspm.fr/~heydari/divers/marianne.html
16. Pour une discussion à propos du nom du 4ème mois du calendrier iranien, voir: M. Heydari-Malayeri, Tishtar, the Iranian Sirius (en préparation).

17. Le fait que le cycle de 220 ans (avec durée moyenne de l'année de 365.2409 jours) peut être divisé en cycles de 29 et 25 ans (220 = 5*29 + 3*25), laisserait entendre que Khâzeni n'avait pas besoin du cycle de 33 ans (365.2424 jours/an). Par conséquent, si aucune autre information émanant de Khâzeni n'est disponible, on peut penser soit qu'il y ait une erreur introduite par les copieurs dans les textes de Khâzeni, soit qu'il ait mal compris ou désapprouvé Khayyâm.

18. Selon plusieurs indices historiques, le calendrier iranien semble avoir été une source d'inspiration pour les créateurs du calendrier révolutionnaire français, qui prônaient le culte de la nature et préféraient donc un système non-religieux et basé sur les saisons. En fait, au cours du siècle des lumières, il y avait un vif intérêt chez les penseurs européens envers les cultures et les civilisations orientales en général. La première traduction dans une langue européenne de l'Avesta, les textes sacrés zoroastriens, a été élaborée par Abraham Anquetil-Duperron en français en 1771. Il est aussi fort probable que les dirigeants de la Révolution française étaient familiarisés avec le calendrier iranien à travers la publication de plusieurs ouvrages. On peut citer, par exemple: Freret, De 1'ancienne année des Perses, 1742, publié dans l'Histoire de l'Académie Royale des inscriptions et belles lettres, tome 16, Paris, 1751 et Gilbert, Nouvelles observations sur l'année des anciens Perses, dans l'Histoire de l'Académie Royale des inscriptions, tome 31, Paris, 1788. Pour plus d'informations, voir l'article de Shafâ (2003) qui met en évidence les éléments perses dans le calendrier révolutionnaire français.




References

Abdollâhi, Rezâ, A.P. 1375 (A.D. 1996), Târix-e Târix dar Irân (L'histoire du calendrier en Iran), Téhéran, Amir Kabir (en persan)

Behruz, Zabih, A.P. 1331 (A.D. 1952), Taqvim va Târix dar Irân (Connaissance des temps et calendriers en Iran), Téhéran, Iran-kudeh, No 15 (en persan)

Birashk, Ahmad, 1993, A Comparative Calendar of Iranian, Muslim Lunar, and Christian Eras for 3000 Years, Mazda Publishers, Bibliotheca Persica, Costa Mesa, California and New York

Biruni, Abu-Rayhân , c. 1000, Athar al-Baqia 'an al-Qurun al-Khalia, translated into English under the title The Chronology of Ancient Nations by Edward C. Sachau, London 1879 (William H. Allen)

de Bloy, François, 1996, The Persian Calendar, J. Brit. Inst. Persian Studies 34, 39
Borkowski, Kazimierz M., 1996/1997, The Persian calendar for 3000 years, Earth, Moon and Planets 74, No 3, 223

Bretagnon, Pierre, Rocher, Patrick, 2001, Du Temps universel au Temps coordonnée barycentrique, Revue du Palais de la Découverte 285, février, p. 39

Briant, Pierre, Histoire de l'Empire Perse, 1996, Fayard, p. 292

Cassidy, Simon, 1996, Error in Statement of Tropical Year

Encyclopedia Iranica, ed. Ehsan Yarshater, Columbia University, Eisenbrauns, Inc., Winona Lake, Indiana

Malakpour, Iradj, 2004, communication privée

Meeus, Jean, 2002, More Mathematical Astronomy Morsels, William-Bell Inc., Richmond, Virginia, Ch. 63

Meeus, Jean, Savoie, Denis, 1992, The history of the tropical year, J. Br. Astron. Assoc. 102, 1

O'Connor, John J., Robertson, Edmund F., 1999, The MacTutor History of Mathematics archive, Omar Khayyam

Morrison, L.V., Stephenson, F.R., 1982, Sun and Planetary System 96, 73, Reidel, Dordrecht

Sayyâd, Mohammad R., 1981 (A.P. 1360), La sequence des intercalations quadrienniales et quinquenniales dans le calendrier Jalâli (en persan), Comptes-rendus de la 12ème Conference des Mathématiques, Université Isfahân, p. 33

Sayyâd, Mohammad R., 2000, Farhang, Quarterly J. of Humanities & Cultural Studies, vol. 12, No. 29-32, Issue topics: Commemoration of Khayyâm, p. 53 (en persan)

Seidelmann, P. K., Guinot, B., Doggett, L.E., 1992, in Explanatory Supplement to the Astronomical Almanac, University Science Books, Mill Valley, Californian, ed. P. K. Seidelmann, p. 80

Shafâ, Shojâedin, 2003, Persian Heritage No 30 (tâbestân-e A.P. 1382), p. 39 (en persan)

Simon, J.L., Bretagnon, P., Chapront, J., Chapront-Touzé, Francou, G., Laskar, J., 1994, Astron. & Astrophy. 282, 663

Stephenson, F. Richard, 2003, Historical eclipses and Earth's rotation, Astronomy & Geophysics 44 (2), 2.22

Stephenson, F.R., Houlden, M.A., 1986, Atlas of Historical Eclipse Maps, page x, Cambridge University Press

Taqizâdeh, S. H., 1938, Old Iranian Calendars, Royal Asiatic Society

Youschkevitch, A.P., Rosenfeld, B.A., 1973, "al-Khayyami", Dictionary of Scientific Biography VIII, p. 323

© Copyright 2004 by M. Heydari-Malayeri
Observatoire de Paris LERMA Last updated 22 March 2010